Question

Let $f:[0,4\pi ]\to [0,\pi ]$ be defined by $f\left(x\right)={\cos }^{-1}\left(\cos x\right).$ The number of points $x\in [0,4\pi ]$ 4satisfying the equation $f\left(x\right)=\frac{10-x}{10}$ is

Explanation

`f:[0,4opi]to[0,pi],f(x)m = cos^(-1)(cosx)`.
For the number of roots of th equation `cos^(-1) (cos x) = (10-x)/(10)` , draw the graph of `y=cos^(-1)(cos x)" and "y=(10-x)/(10)`and find the number points of intersections.

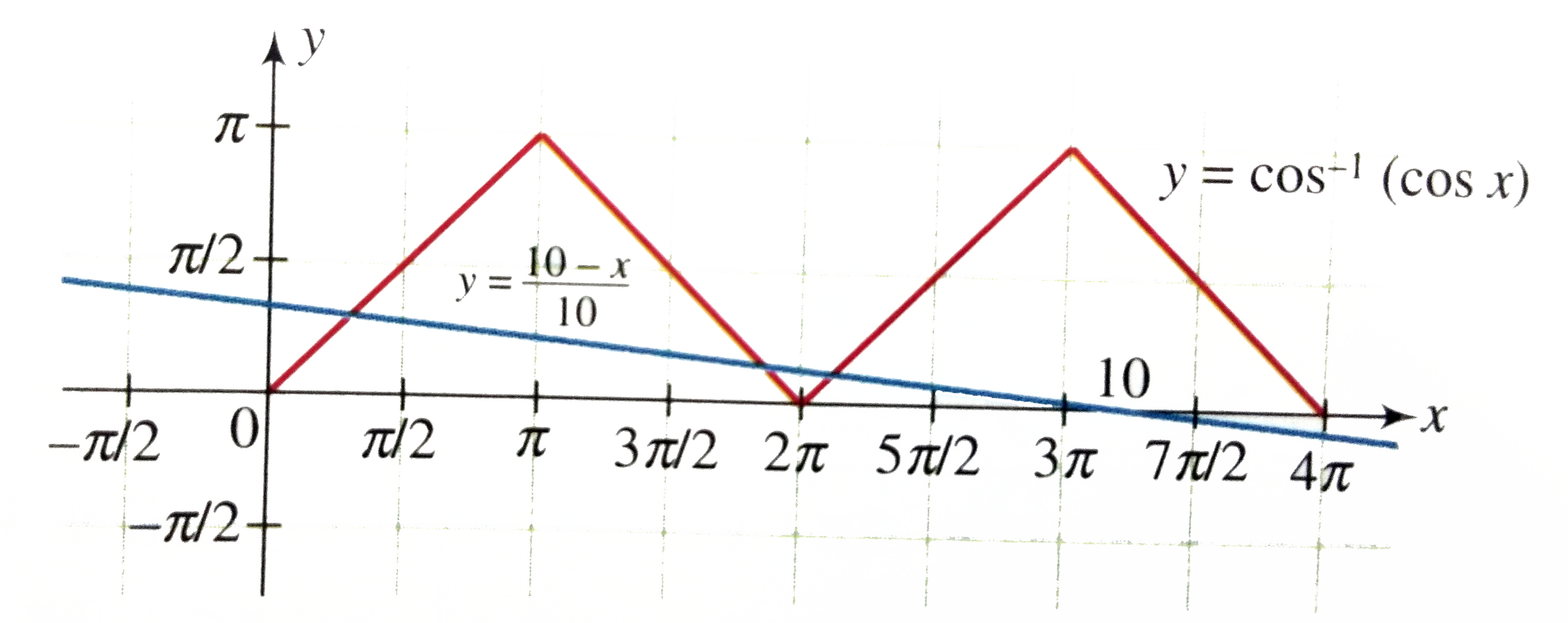
From the graph, the number of solution is 3.