Draw the graph of f(x)=sec−1(secx)
Video Solution
Text Solution
y=sec−1(secx)
⇒ secy=secx
⇒ cosy=cosx
Hence the graph of y=sec−1(secx) is the same as that of y=cos−1(cosx), but excluding points x=(2n+1)π/2,n∈Z, where sec x is not defined.
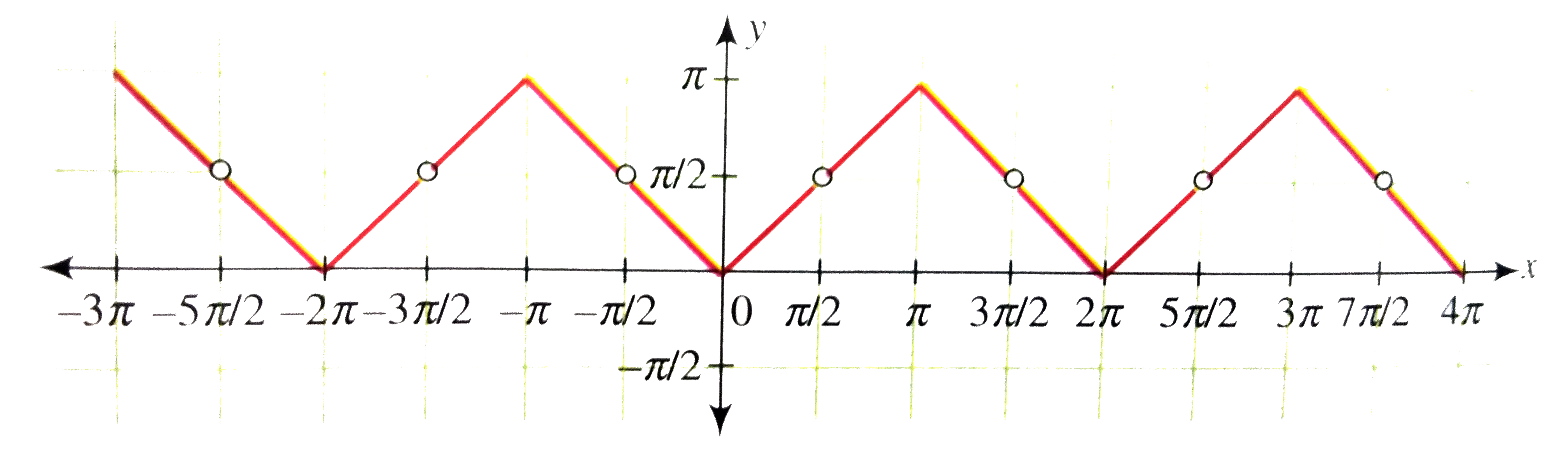
|
Topper's Solved these Questions
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 18 Videos
- GETTING STARTED WITH GRAPHSBook:CENGAGEChapter:GETTING STARTED WITH GRAPHSExercise:Exercise
Explore 18 Videos
- GRAPHICAL TRANSFORMATIONSBook:CENGAGEChapter:GRAPHICAL TRANSFORMATIONSExercise:Exercise
Explore 22 Videos
Similar Questions
Draw the graph of f(x)=x2−3
View SolutionDraw the graph of y=sec−1|x|.
View Solutionxsec−1x
View SolutionDraw the graph of f(x)=cot−1(2−|x|2+|x|).
View SolutionDraw the graph of y=sec−1x+cosec−1x
View SolutionDraw the graph of f(x)=|x−1|x−1.
View SolutionDraw the graph of f(x)=esinx.
View SolutionDraw the graph of f(x)=(x−1)|(x−2)(x−3)|.
View SolutionDraw the graph of f(x)=secx+cosec x,x∈(0,2π)−{π/2,π,3π/2}
Also find the values of 'a' for which the equation secx+cosec x=a has two distinct root and four distinct roots.
View SolutionDraw the graph of f(x)=∣∣∣x2−2x2−1∣∣∣ .
View Solution