Find the sum of roots the equation cos−1(cosx)=[x],[⋅] denotes the greatest integer funtions.
We have cos−1(cosx)=[x]
To find the roods of the equation, we draw the graphs of y=cos−1(cosx) and y=[x] and then find the points of intersection.
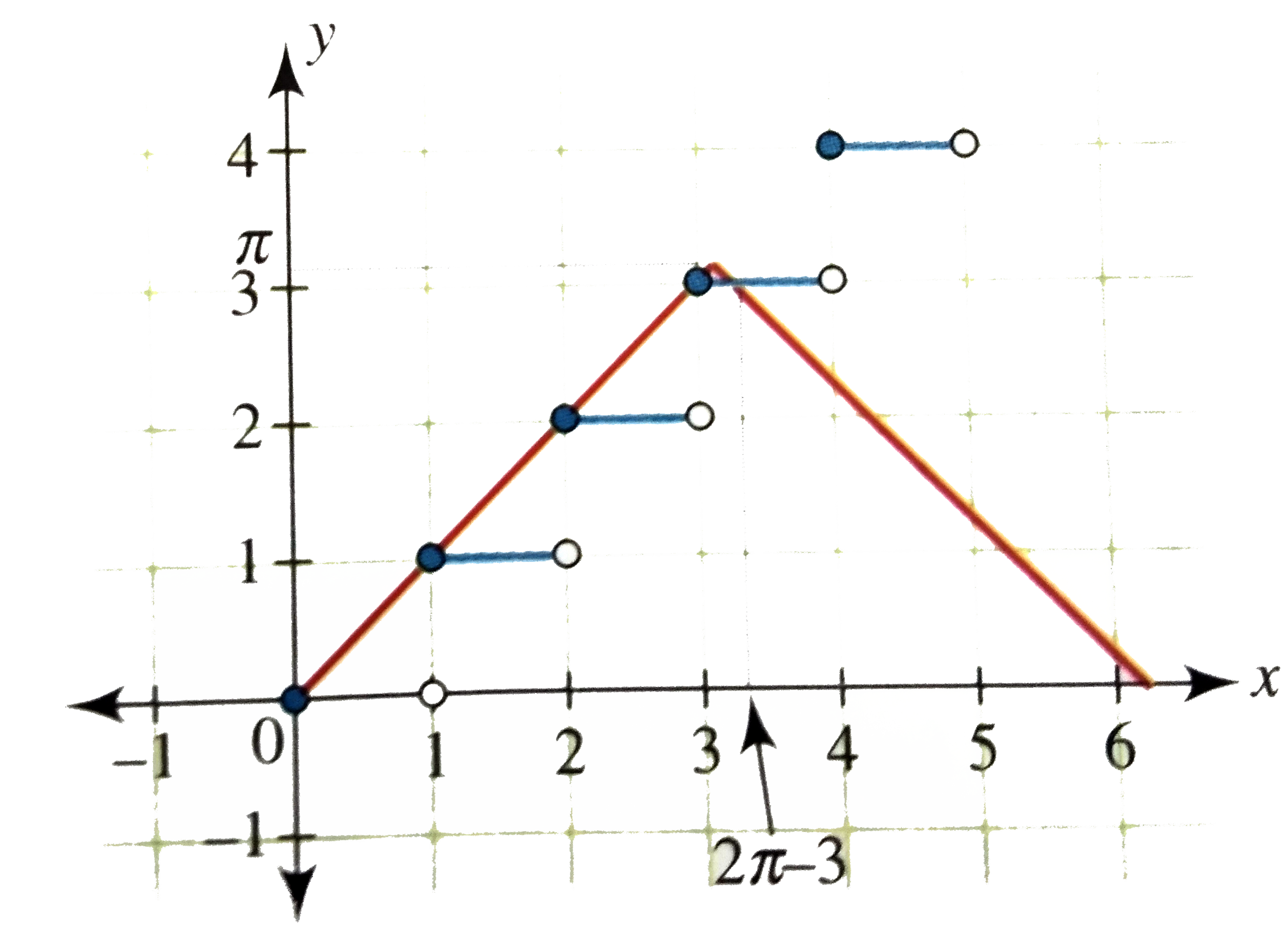
From the graph, roots are 0, 1, 2, 3, and the value ot x for which 3=2π−xorx=2π−3. Hence the sum of roots is 2π+3
Topper's Solved these Questions
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise
18 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
22 Videos
Similar Questions
Knowledge Check
Number of solutions of the equation cos[x]=e2x−1,x∈[0,2π], where[.] denotes the greatest integer function is
A0B1C2Dinfinite
The sum of the roots of the equation cos−1(cosx)=[x]. where [x] denotes greatest integer function, is
View SolutionFind the number of solution of the equations
|cosx|=[x], (where [.] denotes the greatest integer function ).
View SolutionFind the number of solution of the equations
|cosx|=[x], (where [.] denotes the greatest integer function ).
View SolutionNumber of solutions of the equation cos[x]=e2x−1,x∈[0,2π], where[.] denotes the greatest integer function is
View SolutionFind number of solutions for equation [sin−1x]=x−[x], where [.] denotes the greatest integer function.
View SolutionFind number of solutions for equation [sin−1x]=x−[x], where [.] denotes the greatest integer function.
View SolutionFind the period of the function [sin3x]+|cos6x|, where [.] denotes the greatest integer function.
View Solution
