Draw the graph of $y = 2 x^{2} - 1$ and heance the graph of f(x) $= \cos^{- 1} 2 x^{2} - 1)$ .

Text Solution

Verified by Experts

$y = 2 x^{2} - 1$ is an upward parabola having vertex at (0,-1).
It meets the x-axis at $(\pm \sqrt{0})$
For $f (x) = \cos^{- 1} (2 x^{2} - 1)$ to get defined.
$- 1 \leq 2 x^{2} - 1 \leq 1$
$or 0 \leq 2 x^{2} \leq 2$
$or 0 \leq x^{2} \leq 1$
$or - 1 \leq x \leq 1$
Hence the domain of $y = f (x) i s [- 1, 1]$
$N o w f (- 1) = f (1) = \cos^{- 1} = 0 and f (0) = \cos^{- 1} (- 1) = π$
So the inportant points of the graph paper are as follows.

$Now f' (x) = \frac{4 x}{{\sqrt{1 - (2 x^{2} - 1)}}^{2}}$
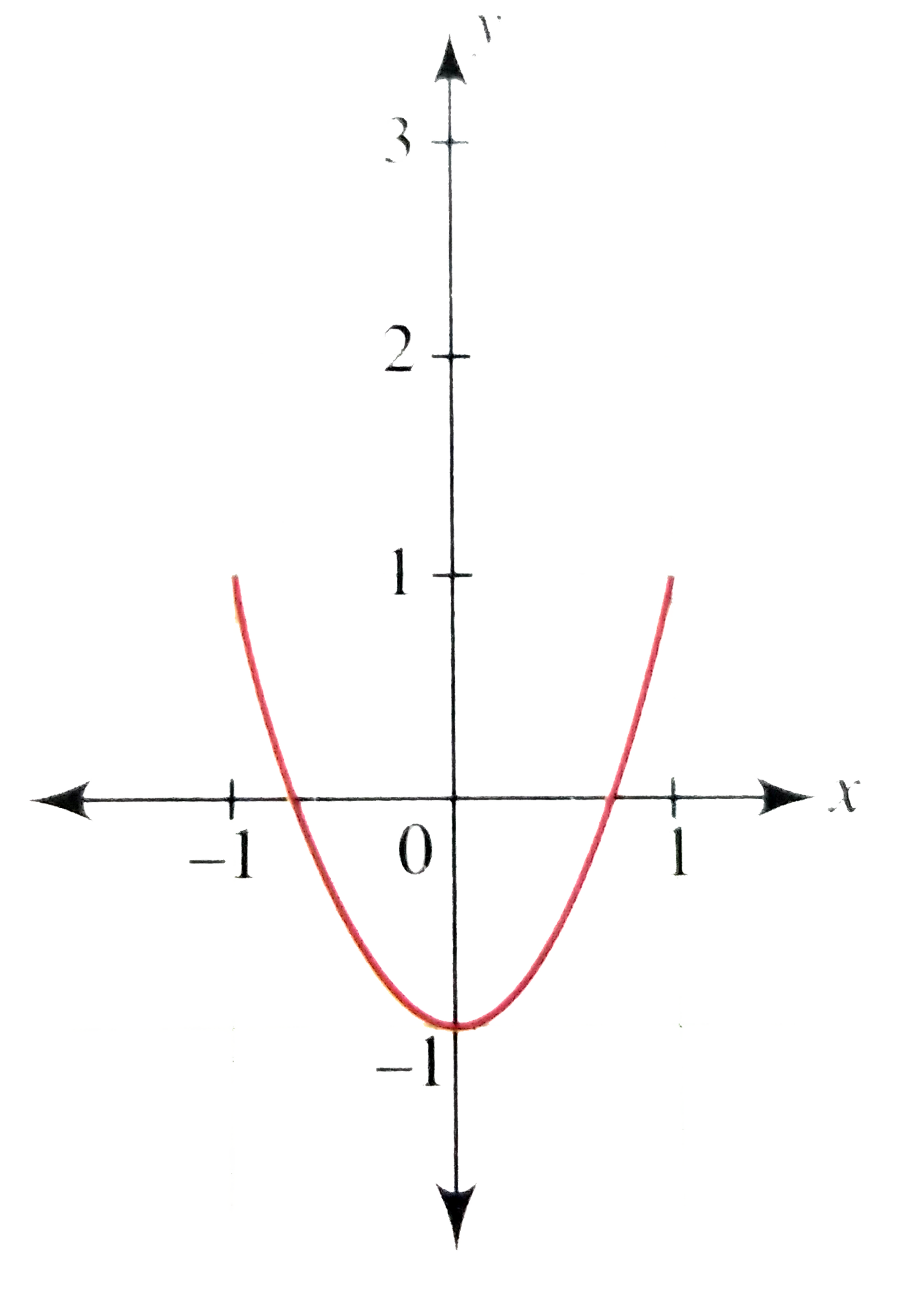
Clearly f'(x) does not exist at x=0, heance f(x) is non-differenctiable at x=0
$Also f' (x) > 0 f or x \in [- 1, 0]$
$and f' (x) < 0 f or x \in (0, 1]$ .
Hence the graph of $y = \cos^{- 1} (2 x^{2} - 1)$ can be drawn as follows.

Updated on:21/07/2023

|

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

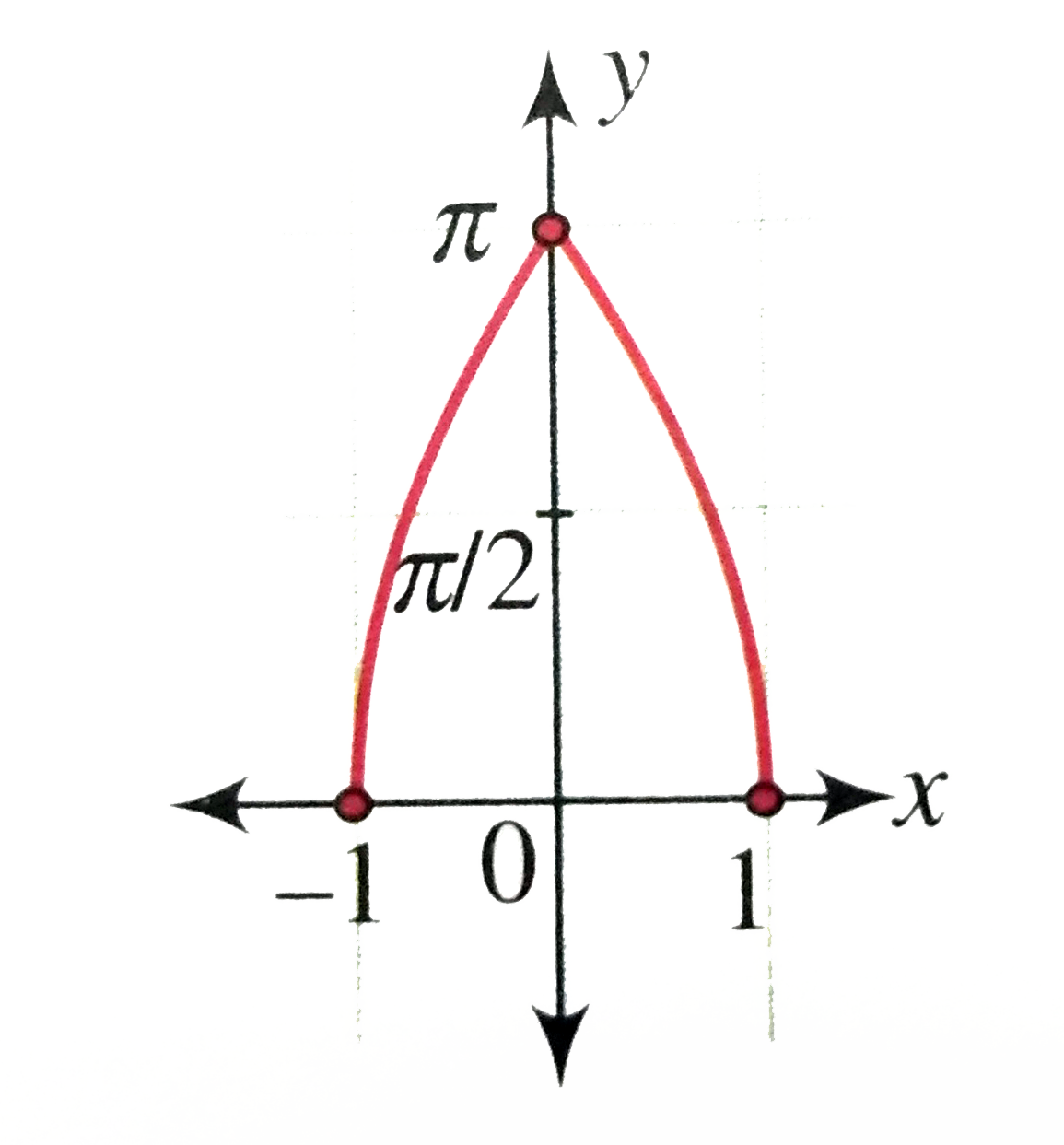
Topper's Solved these Questions

Similar Questions

CENGAGE-GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS-Exercise

Home
Ask Doubt
Profile