The circumcentre and centroid of a triangle are (3,4) and (6,8) respectively. If one of the vertices of the triangle is (0,0), then what is the type of triangle?
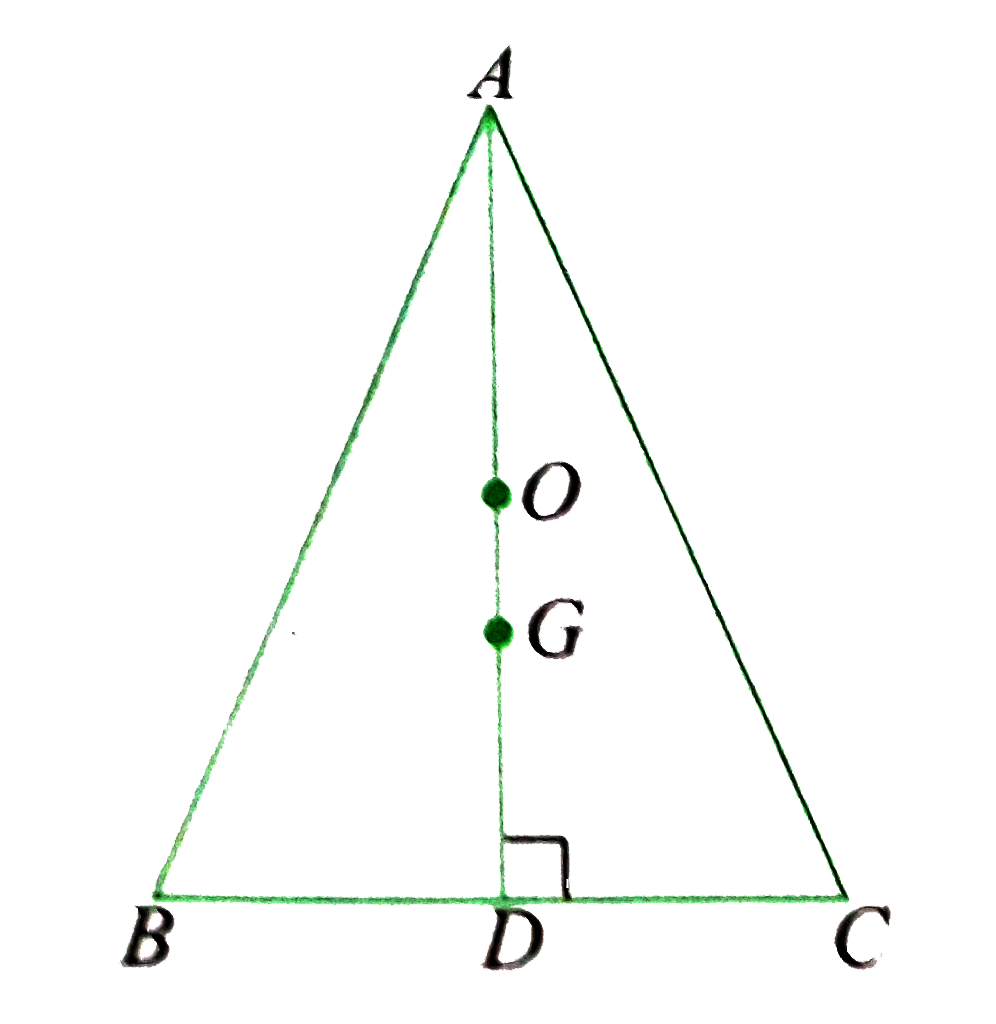
We have vertex A(0,0) circumcentre O(3,4) and centroid G(6,8). Point O lies on the perpendicular bisector (OD) of side BC and point G lies on the median AD.
Now, A O and G are collinear. So median AD and perpendicular bisector (OD) of BC coincide. Thus, AD is the perpendicular bisector of BC. Therefore, triangle ABC is isosceles.
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
If the centroid and orthocentre of a triangle are (3,3) and (-3,5) respectively then the circumcentre is
View SolutionIf a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangle
View Solution
Knowledge Check
If the orthocentre and centroid of a triangle are (-3, 5) and (3, 3) then its circumcentre is
A(6,2)B(0,8)C(6,-2)D(0,4)If the orthocentre and centroid of a triangle are (−3,5,2)and(3,3,4) respectively, then its circumcentre is
A(6,2,5)B(6,2,−5)C(6,−2,5)D(6,−2,−5)The circumcentre of the triangle with vertices (0, 0), (3, 0) and (0, 4) is
A(1, 1)B(2, 3/2)C(3/2, 2)Dnone of these
If a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangle
View SolutionIf the centroid and two vertices of a triangle are (4.−8),(−9,7),(1,4) respectively. Then the area of the triangle ( in sq.units) is
View SolutionIf the circumcentre of a triangle lies outside the triangle, then what type of triangle is it ?
View SolutionIf midpoints of the sides of a triangle are (0, 4), (6, 4) and (6, 0), then find the vertices of triangle, centroid and circumcentre of triangle.
View Solutioncircumcentre of the triangle whose vertices are (1,0),(3,0) and (1,6) is
View Solution
