Question

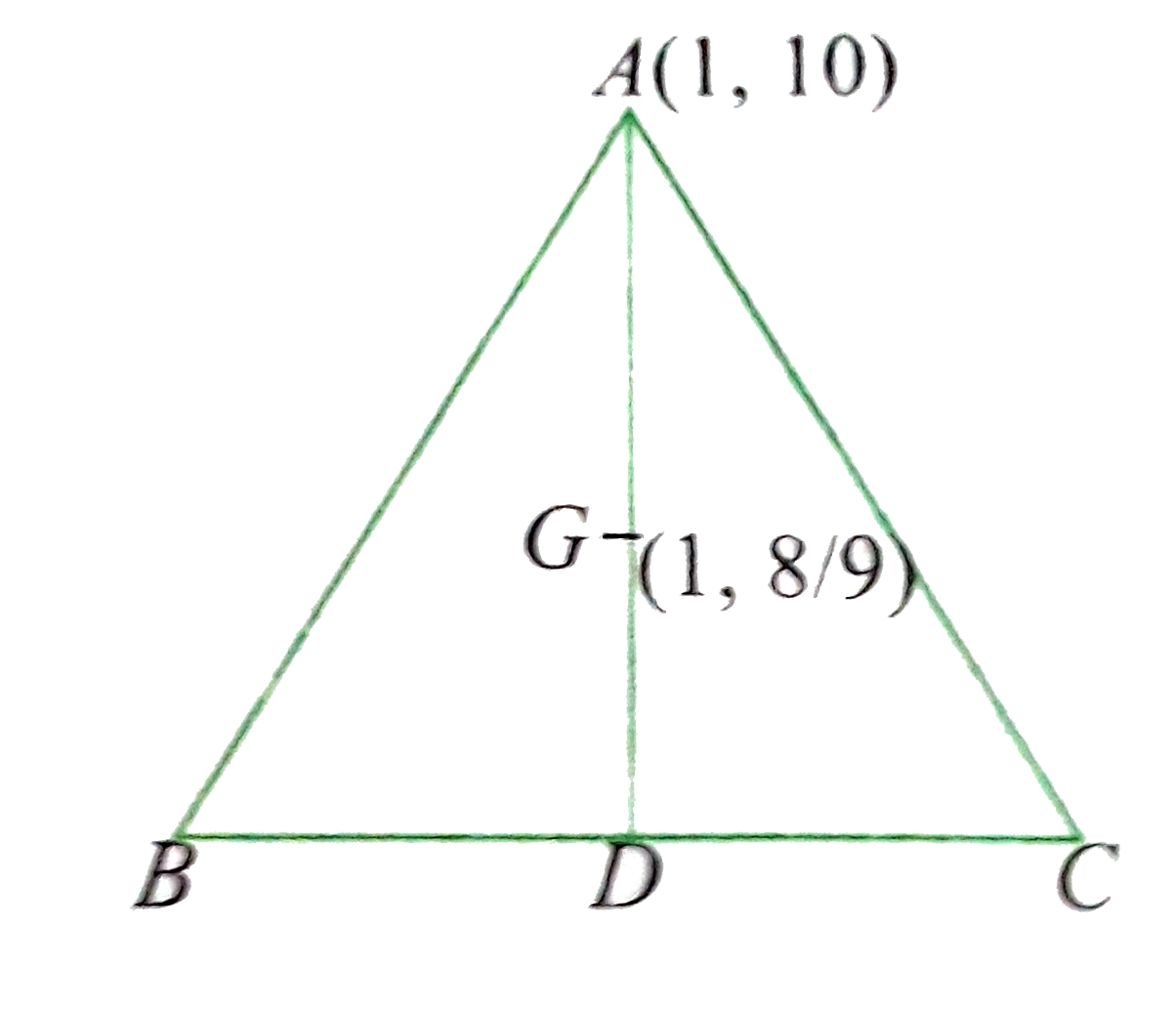
If a triangle $ABC,A\equiv (1,10),$
circumcenter $\equiv (-\frac{1}{3},\frac{2}{3}),$
and orthocentre $\equiv (\frac{11}{4},\frac{4}{3})$
, then the coordinates of the midpoint of the side opposite to $A$
are
$(1,-\frac{11}{3})$
(b)
$(1,5)$

$(1,-3)$
(d) $(1,6)$

Options

A. `(1,-11//3)`
B. `(1//5)`
C. `(1,-3)`
D. `(1,6)`

Answer

A

Explanation

Circumcenter `O-=(-1//3,2//3)` and orthocenter `H-=(11//3,4//3)`

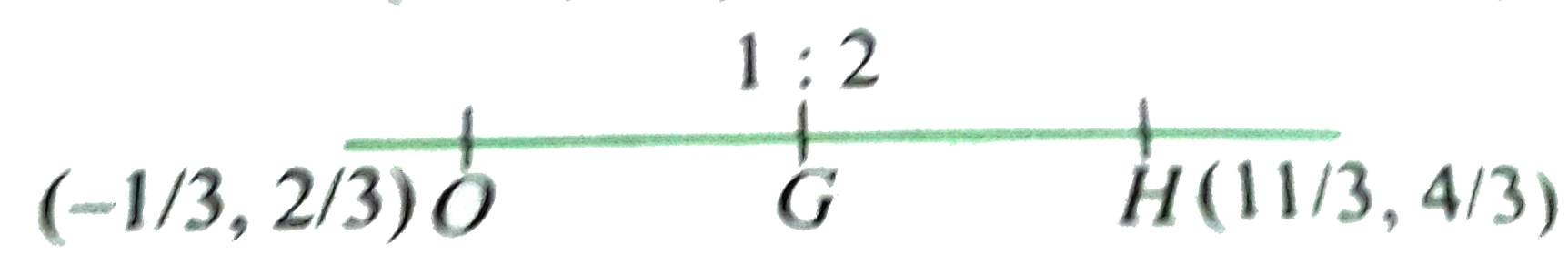
Therefore the coordinates of G are `(1,8//9)`. Now,the point A is `(1,10)` as G is `(1,8//9)`.
Also, `AD:DG=3:1`,
`therefore D-=((3-1)/(3-1),(8//3-10)/(3-1))-=(1,-11//3)`
`therefore D=(3-1)/(2)=1,D_(y)=(8//3-10)/(2)=-11/3`
Hence, the coordinates of the midpoint of BC are `(1,-11//3)` .