Let ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to
3
2
1
0
The correct Answer is:D
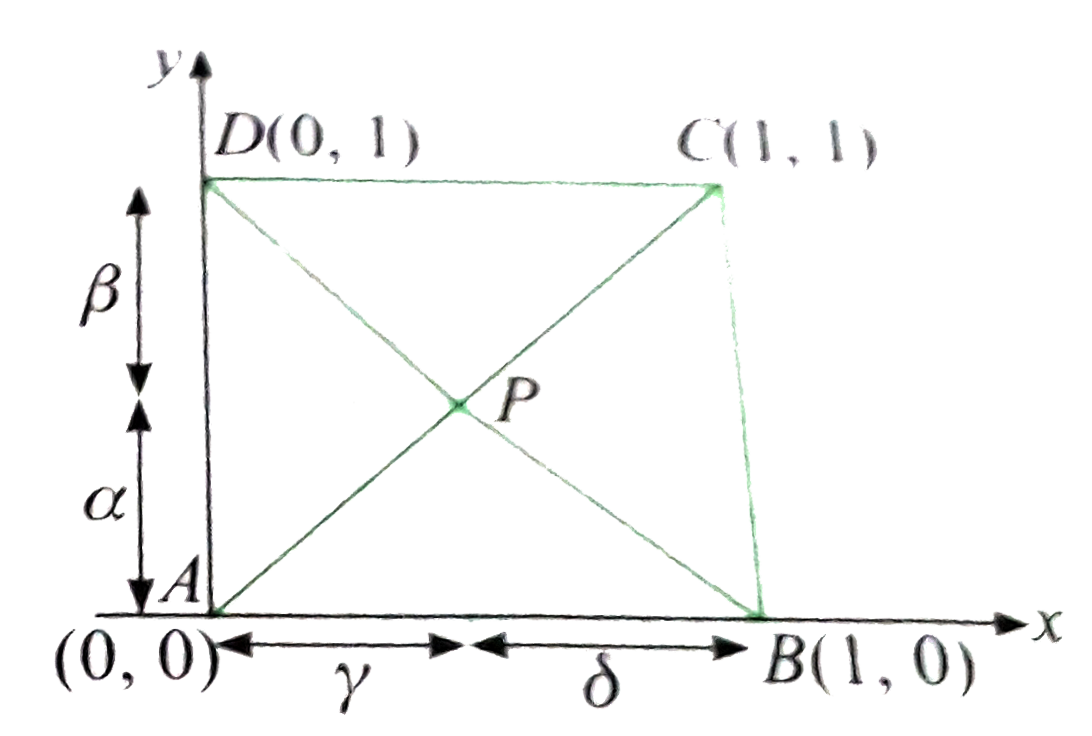
(PA)2−(PB)2+(PC)2−(PD)2
=(α2+γ2)−(α2+δ2)+(δ2+β2)−(γ2+β2)=0
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Matrix)
4 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Numerical)
12 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)
13 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Let ABCD is a square with sides of unit length. Points E and F are taken om sides AB and AD respectively so that AE= AF. Let P be a point inside the square ABCD.The maximum possible area of quadrilateral CDFE is-
View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square is
View Solution
Knowledge Check
Let ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square isA√10/3B√13/3C√11/3D2/√3Let ABCD be a square of side length 2 units. Let C1 be the incircle and C2 be the circumcircle of the square ABCD. If P is a point on C1 and Q is a point on C2, the value of PA2+PB2+PC2+PD2QA2+QB2+QC2+QD2 is
AA) 0.75BB) 1.25CC) 1DD) 0.5
If P be any point in the plane of square ABCD, prove that
PA2+PC2=PB2+PD2
View SolutionIf P be any point in the plane of square ABCD, prove that
PA2+PC2=PB2+PD2
View SolutionLet ABCD be a parallelogram of area 124cm2 If E and F are the mid-points of the sides AB and CD respectively then find the area of the parallelogram AEFD
View SolutionLet ABCD be a parallelogram of area 124cm2. If E and F are the mid-points of sides AB and CD respectively, then find the area of parallelogram AEFD.
View SolutionLet ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and CD respectively, then find the area of parallelogram AEFD
View SolutionP is a point inside the rectangle ABCD such that PA=2, PB=9, PC=10 & PD=√k then k is equal
View Solution
