Let ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
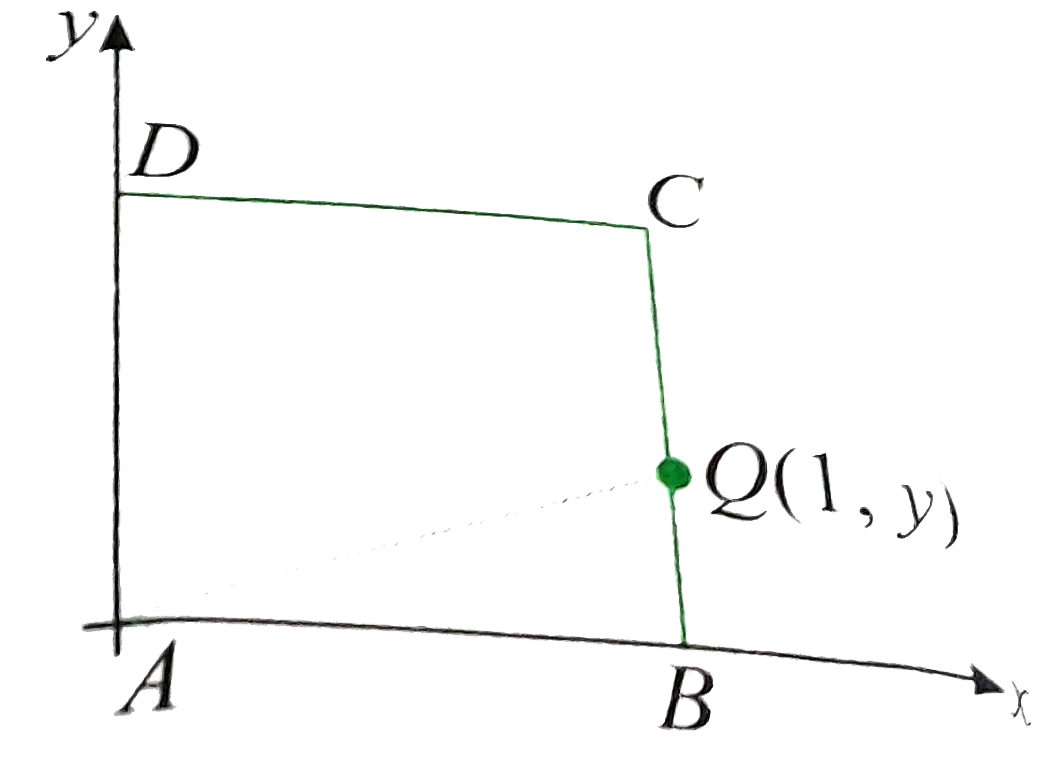
Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square is
√10/3
√13/3
√11/3
2/√3
The correct Answer is:B
12y(1)=13(1)
or y=23
∴AQ=√(1)2+(23)2=√133
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Matrix)
4 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Numerical)
12 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)
13 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Let ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to
View SolutionLet ABCD is a square with sides of unit length. Points E and F are taken om sides AB and AD respectively so that AE= AF. Let P be a point inside the square ABCD.The maximum possible area of quadrilateral CDFE is-
View Solution
Knowledge Check
Let ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal toA3B2C1D0ABCD is a square Points E(4,3) and F(2,5) lie on AB and CD, respectively,such that EF divides the square in two equal parts. If the coordinates of A are (7,3),then the coordinates of other vertices can be
A(7,2)B(7,5)C(−1,3)D(−1,5)
Let ABCD be a parallelogram of area 124cm2 If E and F are the mid-points of the sides AB and CD respectively then find the area of the parallelogram AEFD
View SolutionLet ABCD be a parallelogram of area 124cm2. If E and F are the mid-points of sides AB and CD respectively, then find the area of parallelogram AEFD.
View SolutionLet ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and CD respectively, then find the area of parallelogram AEFD
View SolutionABCD is a square Points E(4,3) and F(2,5) lie on AB and CD, respectively,such that EF divides the square in two equal parts. If the coordinates of A are (7,3),then the coordinates of other vertices can be
View SolutionLet D(x4,y4) be a point such that ABCD is a square and M and P are the midpoints of the sides BC&CD respectively, then
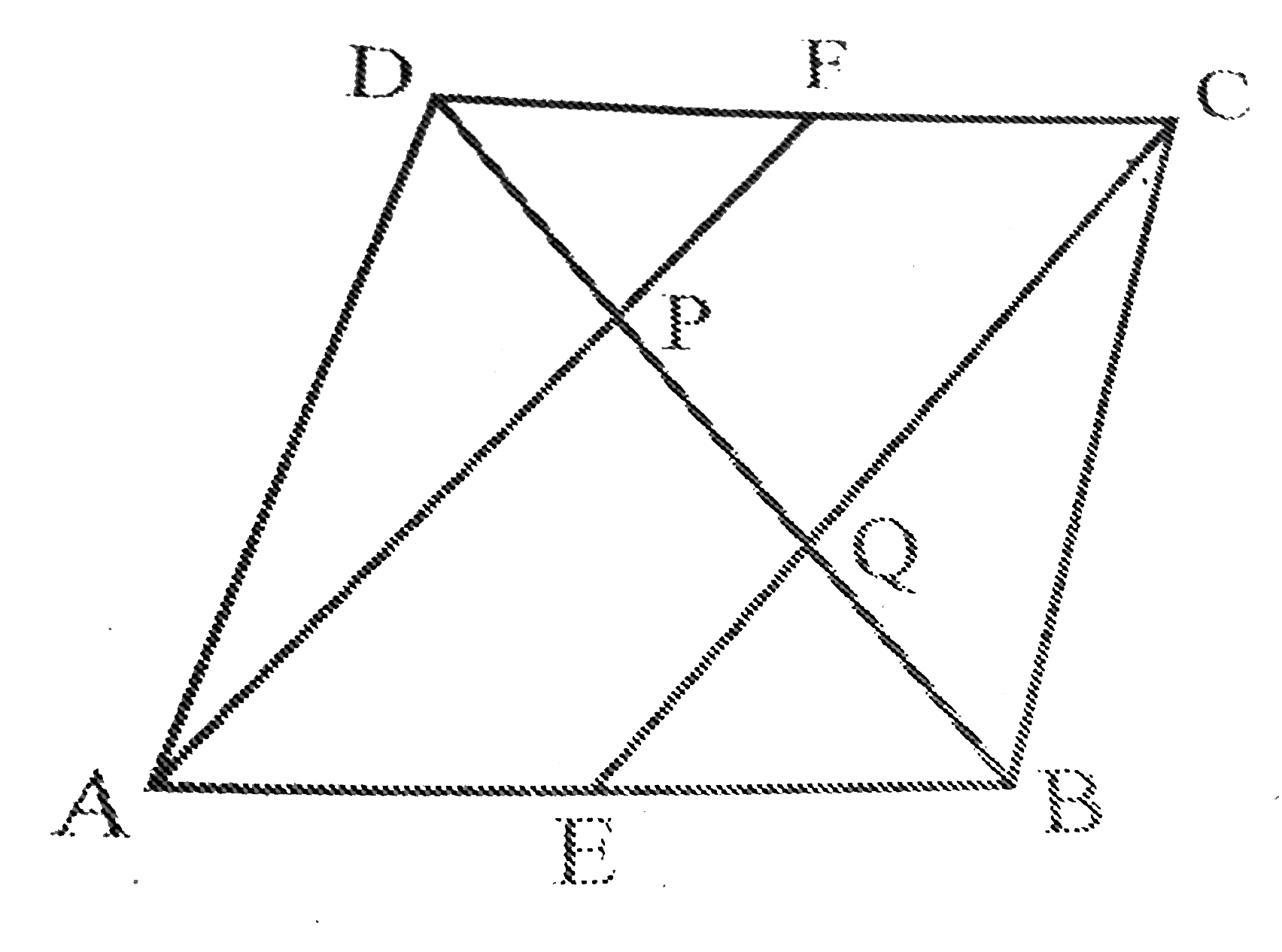
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.
View Solution
