An initially empty beaker, in the shape of a cylinder with cross sectional area A, is left out in th rain. The raindrops hit the beaker vertically downward with speed v. The rain continues at a constant rate, so the height of the water in the beaker h(t) increases with time t at a rate dh/dt=u, where u is small compared to v. The raindrops quickly come to rest inside the beaker, so we can neglect any kinetic energy of the water that has collected in the beaker. Let p denote the density of water (i.e., the mass per unit volume)
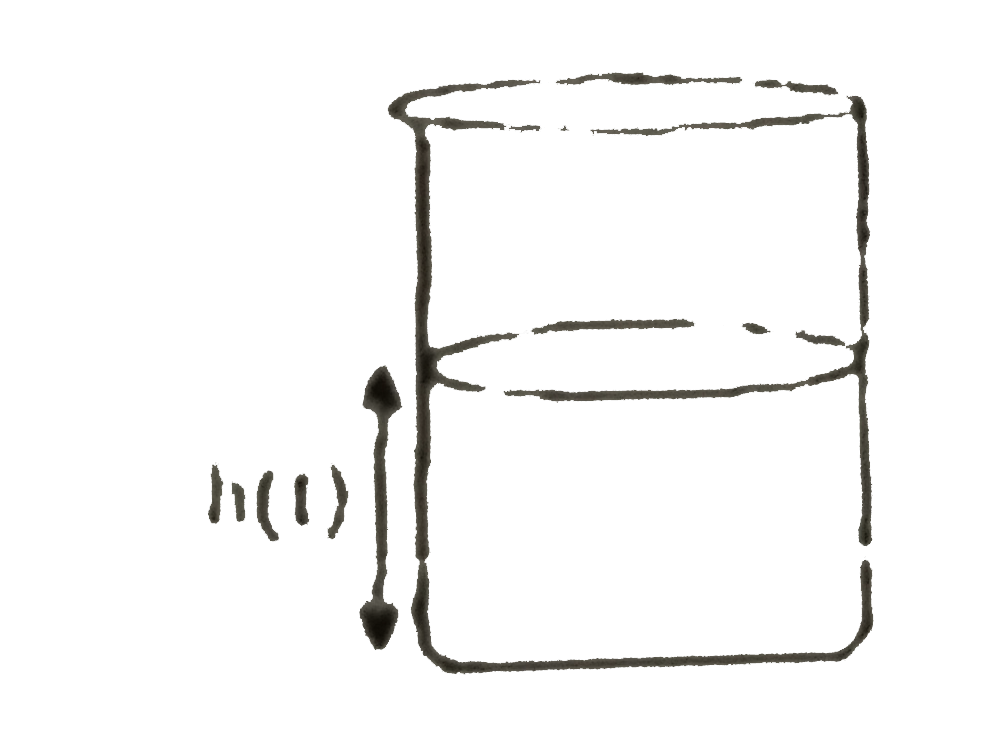
An initially empty beaker, in the shape of a cylinder with cross sectional area A, is left out in th rain. The raindrops hit the beaker vertically downward with speed v. The rain continues at a constant rate, so the height of the water in the beaker h(t) increases with time t at a rate dh/dt=u, where u is small compared to v. The raindrops quickly come to rest inside the beaker, so we can neglect any kinetic energy of the water that has collected in the beaker. Let p denote the density of water (i.e., the mass per unit volume) If the beaker is placed on a weighing scale, while the beaker is wstill in the rain, the impact of the raindrops on the beaker will cause the reading on the scale increased by the impact of the raindrops ? (Neglect the effect of raindrops that hit the scale directily).
If the beaker is placed on a weighing scale, while the beaker is wstill in the rain, the impact of the raindrops on the beaker will cause the reading on the scale increased by the impact of the raindrops ? (Neglect the effect of raindrops that hit the scale directily).

A

pAv2g

B

pAu2g

C

pAuVg

D

pAuv2g

Text Solution
Verified by Experts

The mass in the beaker is given by the product of the density p ahnd the volume V=Ah that is filled, i.e.
m=pAh
When the height changes at a rate dh/dt=w, the mass changes at the rate
dmdt=pAdhdt=pAu
(b) The height of the center of mass of the water in the beaker is at ycm h/2 (at least if we assume incompressible fund, i.e. a constant density, which is a very good approx imation for water). The rate at which the height of the center of mass increases is
dycmdt=12dhdt=w2
(c) The center of mass is moving upward because more water is added to the beaker.i.e. as time evolves we are talking about a whole sequence of physical systems, not about the center of mass of a fixed given system. At any given time, the water in the beaker is at rest and hence its momentum vanishes. It is therefore incorrect to conclude that the water in the beaker has a total vertical momentum.
(d) The raindrops enter the beaker with a speed v and then quickly come to rest inside the beaker. Consider a short time interval Δt, and consider the system that consists of the beaker, all the water that has landed in the beaker by the beginning of the time intergval, plus the water that will come to rest inside the beaker during the time interval. During the time interval Δt the height of the water in the beaker will increase by Δh=wΔt, so the volume of water that will come to rest during the time interval is ΔV=Aδh=AwΔt, shown shaded in the diagram on the right. The mass of this water is ΔM=pΔV=pAwΔt. Taking the vertical direction as the y-direction, the momentum of this water at the beginning of the interval is →Pi
=[0,−vΔM,0]=[0,−pAwvΔt,0]. The final momentum is zero, after the raindrops come rest, so
→Fext=Δ→PΔt=−→PiΔt=[0,pAw,0]
ocr_image
From the diagram one can see that Fext=N
M(t)g, where M(t) is the total mass of the beaker and the water in it at time t.So,
N=M(t)g+pAwv
By Newton's third law the beaker exerts a force of equal magnitude on the scale, which detemines its reading the first term is just the weight of the system, while the question asks by how much the reading is increased by the impact of the raindrops. Thus the second term in the above expression is the answer to the question. ΔN=pAwv
Since, scales often read in units of mass rather than force, it would be equally correct to say that the mass reading would be increased by
ΔM=pAwv/g

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • An initially empty beaker, in the shape of a cylinder with cross sectional area A, is left out in th rain. The raindrops hit the beaker vertically downward with speed v. The rain continues at a constant rate, so the height of the water in the beaker h(t) increases with time t at a rate dh/dt=u, where u is small compared to v. The raindrops quickly come to rest inside the beaker, so we can neglect any kinetic energy of the water that has collected in the beaker. Let p denote the density of water (i.e., the mass per unit volume)
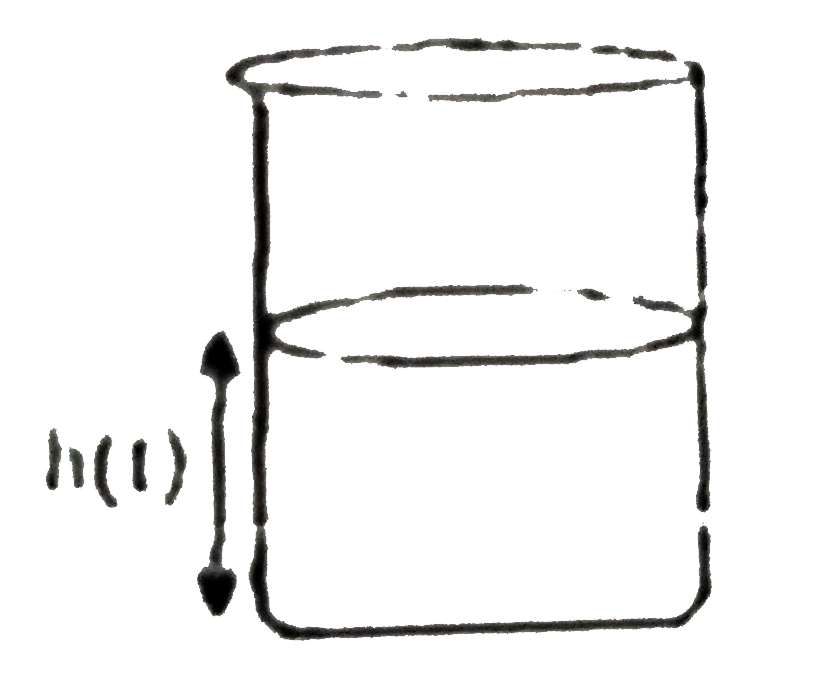
    ocr_image
    Choose the incorrect option.

    ARate at which the mass of the water in the beaker increaes with time is Pau.
    BAt a given time the water in the beaker has total vertical momentum.
    CThe mass of the water in the beaker at a given time is pA
    Dnone of the above options

  • An initially empty beaker, in the shape of a cylinder with cross sectional area A, is left out in th rain. The raindrops hit the beaker vertically downward with speed v. The rain continues at a constant rate, so the height of the water in the beaker h(t) increases with time t at a rate dh/dt=u, where u is small compared to v. The raindrops quickly come to rest inside the beaker, so we can neglect any kinetic energy of the water that has collected in the beaker. Let p denote the density of water (i.e., the mass per unit volume)
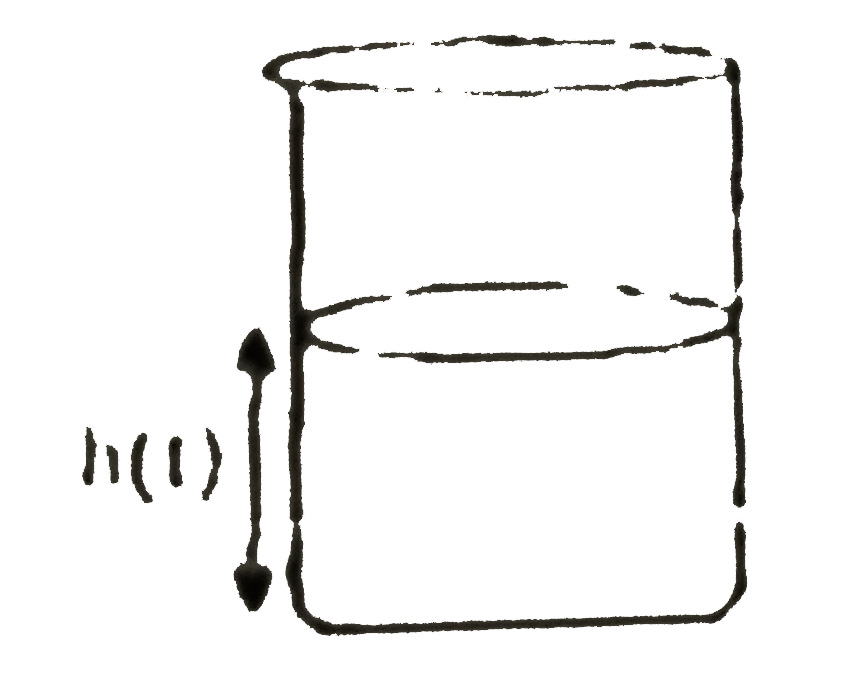
    ocr_image
    Ley ycm(t) denote the height of the centre of mass of all the water that has collected in the beaker by time t. what is the rate at which this height increaes (i.e. dy(cm)/dt?

    Au
    Bu2
    CVolume strength
    Dv2

  • A beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:

    A0
    Bhρg
    Chρg3
    D2hρg