A particle of mass m kept at the origin is subjected to a froce →F=(pt−qx)ˆi where t is the time elapsed and x is the x co-ordinate of the position of the particle. Particle starts its motion at t=0 with zero initial velocity. If p and q are positive constants, then:
The acceleration of the particle will continously keep on increasing with time.
Particle will execute simple harmonic motion.
The force on the particle will have no upper limit.
The acceleration of particle will very sinusoidally with time.
F=pt−qx
⇒a=1m(pt−qx)⇒dadt=[p−qv]m
⇒d2adt2=−qma[=−ω2a]⇒ω=√qm
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A particle of mass m is subject to a force (F) .Find the time dependent position x(t) of the particle for the following two cases : (a) F(x)=kx, with k>0, the initial position is x0, and the initial speed is zero. (b) F(v)=−bv2 and the initial position is zero,and the initial speed is v0.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View Solution
Knowledge Check
A particle of mass m is subjected to a force →F=F0[cos(t)ˆi+sin(1)ˆj]. If initially (t=0) the particle was at rest, the kinetic energy of the particle as a function of time is given by:
AF20m(1−cos(2t))BF20m(1−cost)CF20msin(t)DF20mtThe position vector of a particle is r=asinωtˆi+acosωtˆj
The velocity of the particle isAparallel to position vecorBperpendicular to position vectorCdirected towards originDdirected awa from the originA particle starts moving with constant, velocity v=ms, from position x=5m The position time graph will be
A B
B C
C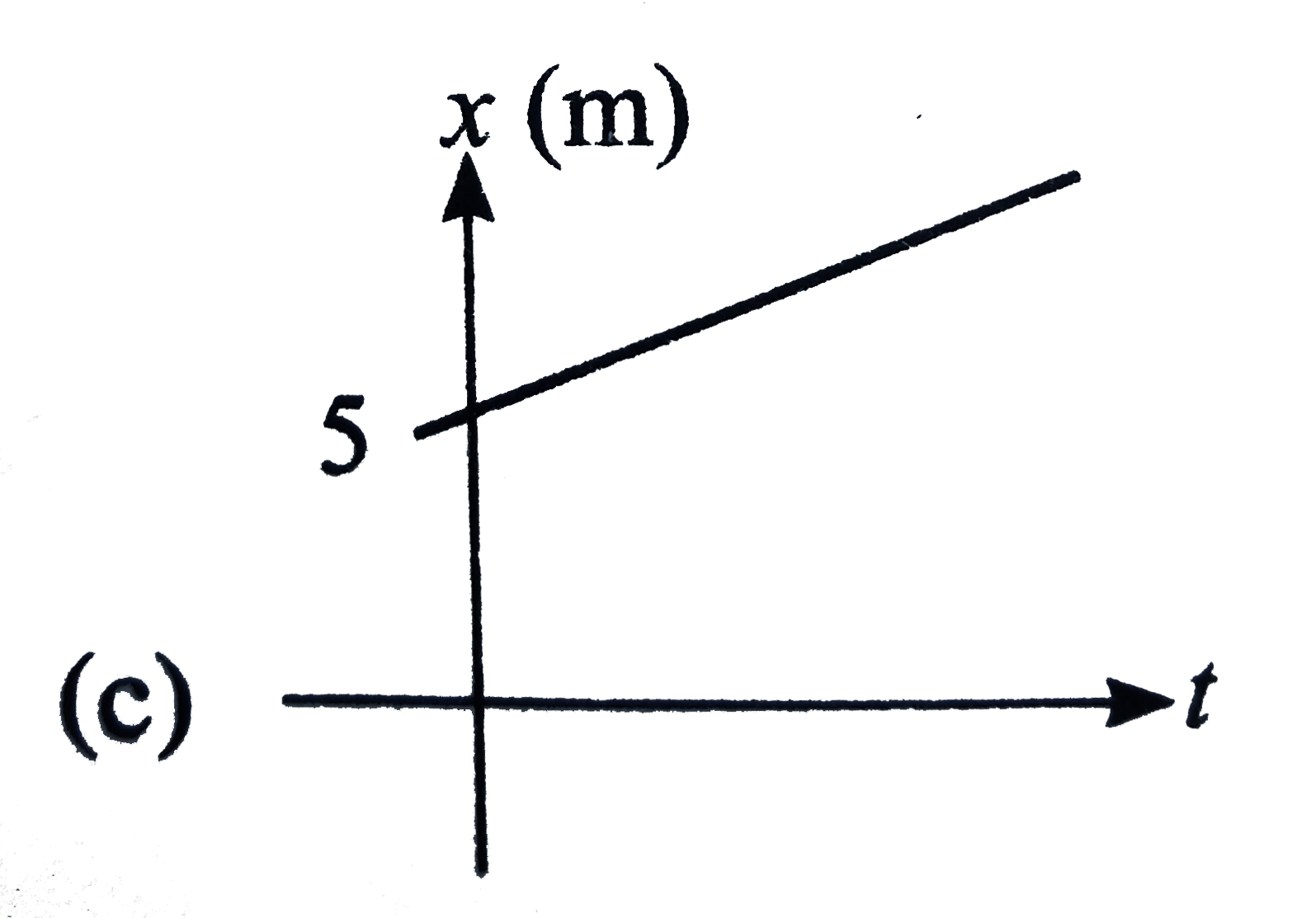 D
D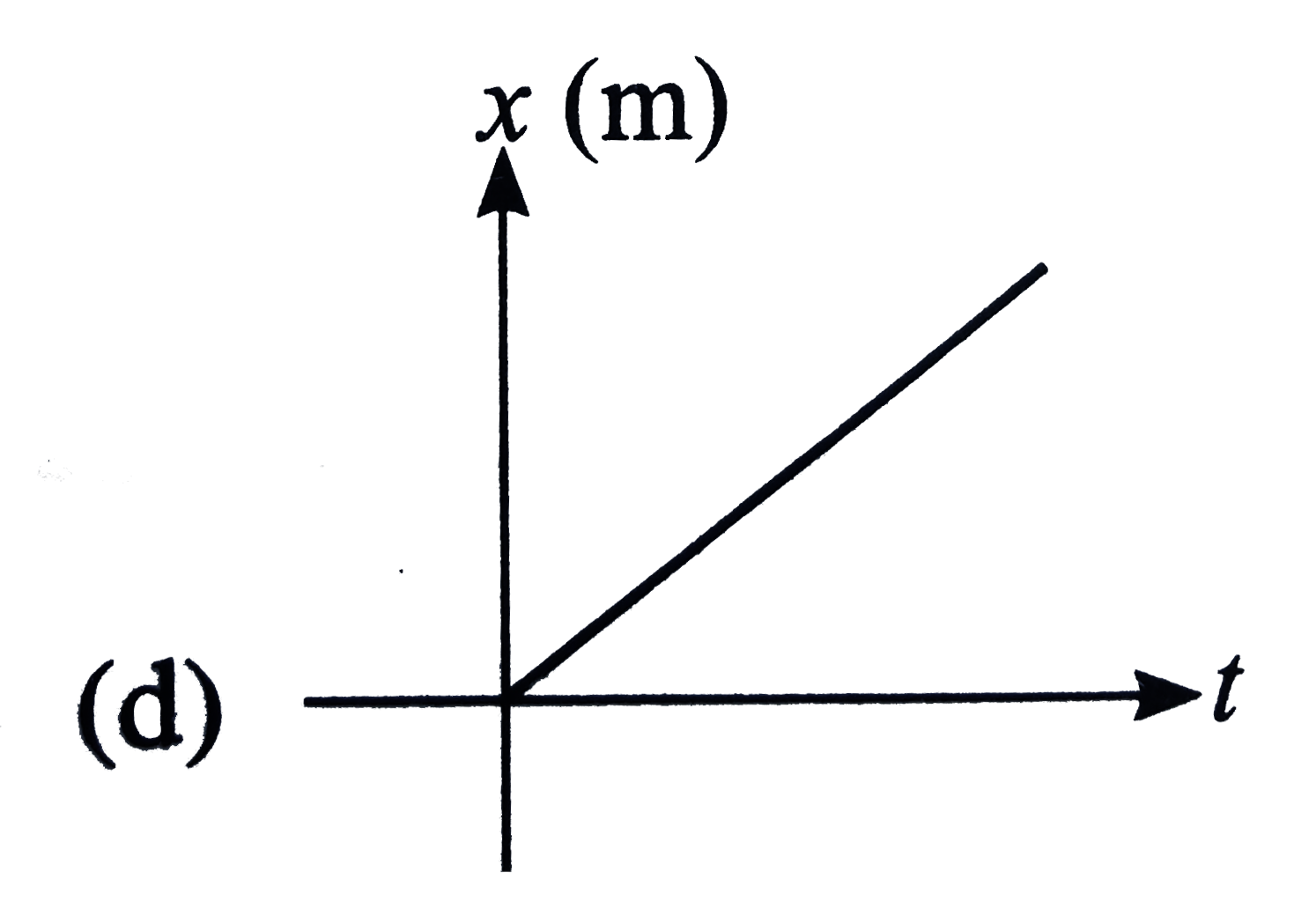
A charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionA particle of charge q and mass m is subjected to an electric field E=E0(1−ax2) in the x - direction, where a and E0 are constants. Initially the particle was at rest at x = 0. Other than the initial position the kinetic energy of the particle becomes zero when the distance of the particle from the origin is :
View SolutionA particle of mass 3 kg moves under a froce of [4ˆi+8ˆj+10ˆk] newton . Calcutale the acceleration (as vector) to which the particle is subjected. If the particle starts from rest and was at the origin initially. What are its new co - ordinates after 3 s?
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The maximum value of position co-ordinate of particle on positive x-axis is
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at the origin .
View Solution
