A cone of radius r and height h is kept on a turntable rotating with an angular velocity. The friction between te table and the cone is sufficient so that the cone does not slide. The distance between the axis of the cone and the axis of turntable is R(R>>r). the maximum value of ω for which the cone does not topple is √xgrRh, calculate x.
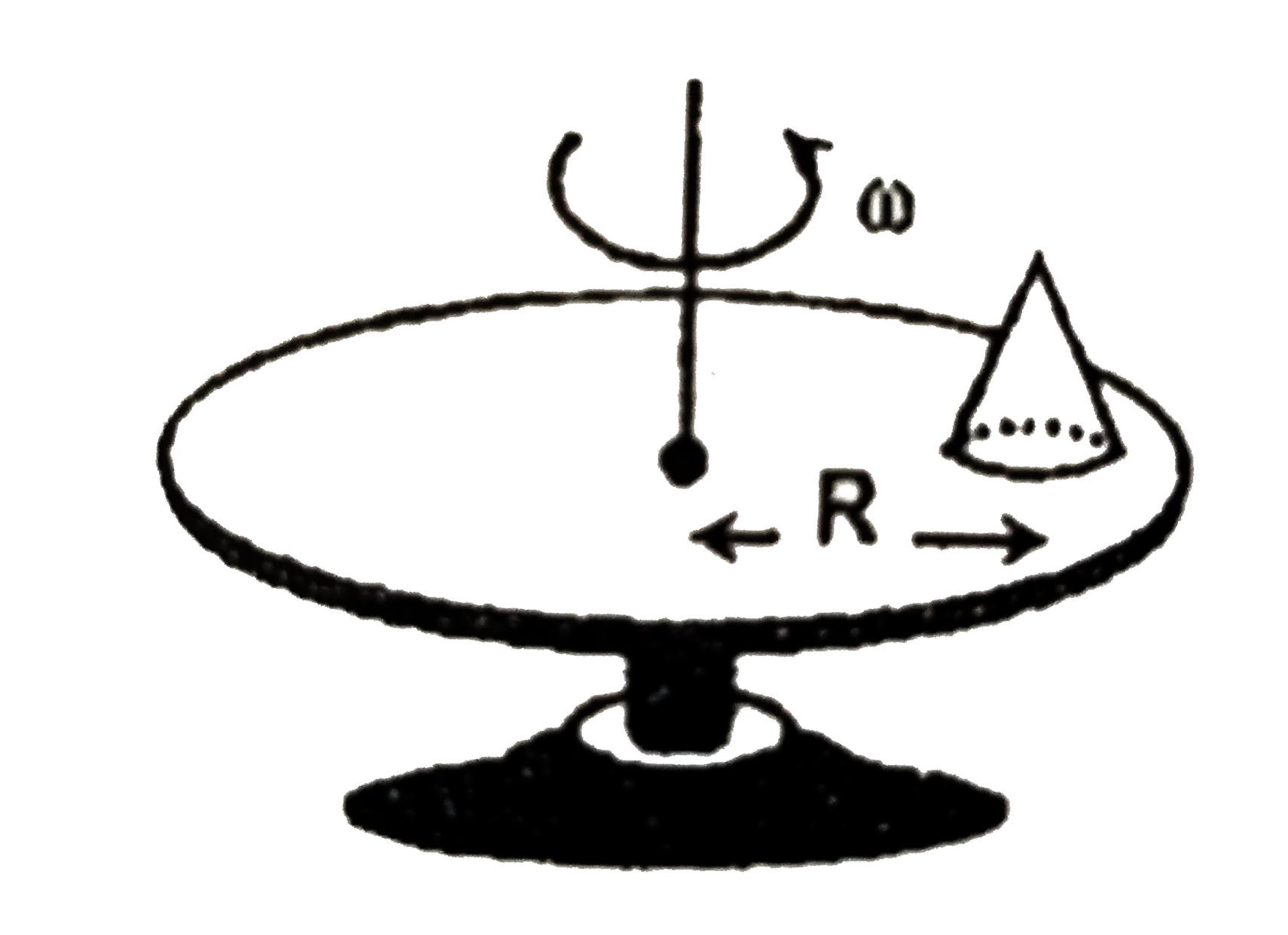
mω2R(h4)=mgr⇒ω=√4grRn
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.
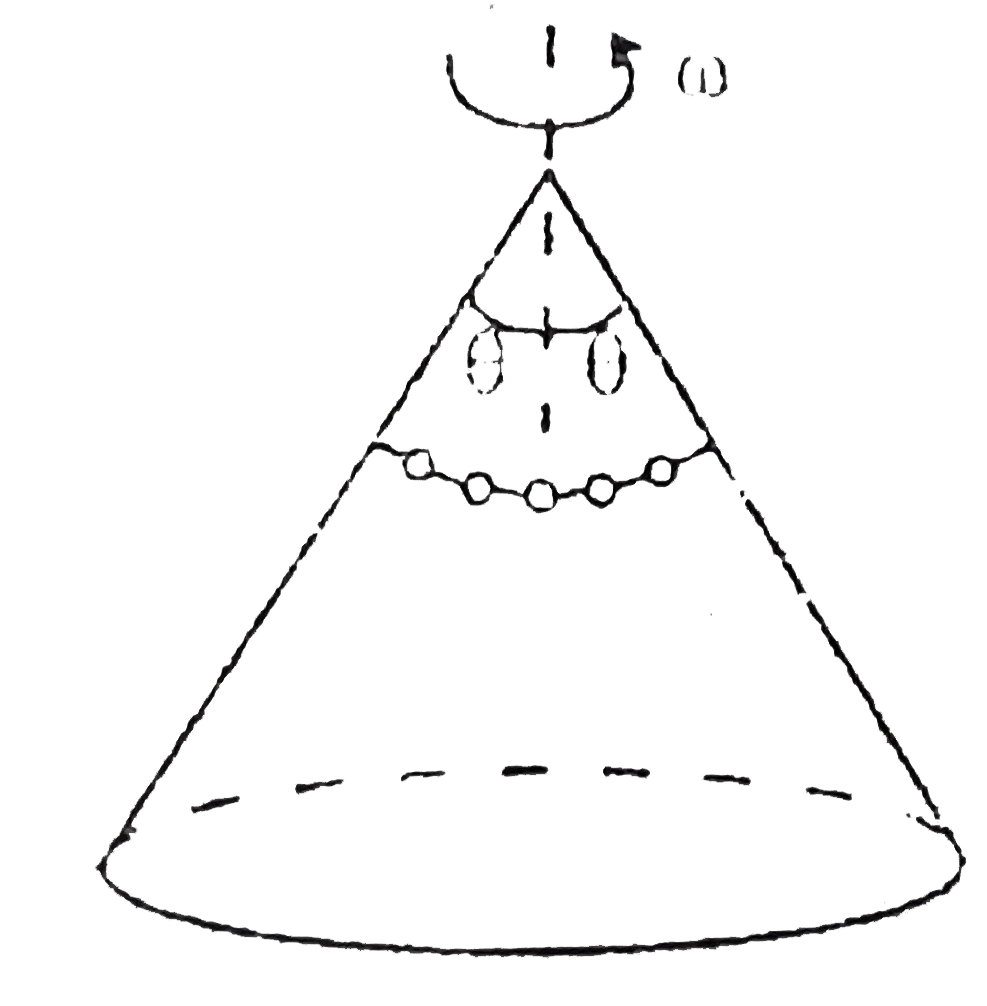
View SolutionA chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.

View Solution
Knowledge Check
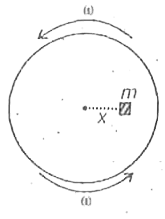
A rough horizontal plate rotates with angular velocity ω about a fixed verticle axis. A particle or mass m lies on the plate at a distance 5a4 from this axis. The coefficient of friction between the plate and the particle is 13 . The largest value of ω2 for which the oparticle will continue to be at rest on the revolving plate is
Ag3aB4g5aC4g9aD4g15a
A particle of mass m is placed over a horizontal circular table rotating with an angular velocity ω about a vertical axis passing through its centre. The distance of the object from the axis is r. Find the force of friction f between the particle and the table.
View SolutionA cylinder with radius R spins about its horizontal axis with angular speed ω. There is a small block lying on the inner surface of the cylinder. The coefficient of friction between the block and the cylinder is μ. Find the value of ω for which the block does not slip, i.e., stays at rest with respect to the cylinder.
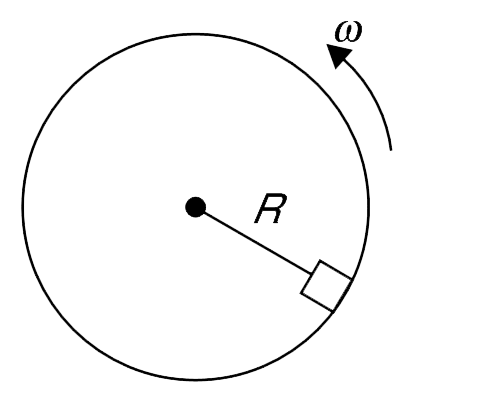
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip

View SolutionA rough horizontal plate rotates with angular velocity ω about a fixed vertical axis. A particle or mass m lies on the plate at a distance 5a4 from this axis. The coefficient of friction between the plate and the particle is 13 . The largest value of ω2 for which the particle will continue to be at rest on the revolving plate is
View SolutionA cylinder rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocity, ω, the cylinder falls off the disc, if the distance between the axes of the disc and cylinder is R, and the coefficient of friction μ>D/h where D is the diameter of the cylinder and It is its height.

View SolutionA cylinder rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocity, ω, the cylinder falls off the disc, if the distance between the axes of the disc and cylinder is R, and the coefficient of friction μ>D/h where D is the diameter of the cylinder and It is its height.

View Solution
