Two bodies of masses m1 and m2 initially at rest at infinite distance apart move towards each other under gravitational force of attraction. Their relative velocity of approach when they are separated by a distance r is (G= universal gravitational constant.)Solution in Telugu
[2G(m1−m2)r]1/2
[2G(m1+m2)r]1/2
[r2G(m1m2)]1/2
[r2Gm1m2]1/2
Initially when the two masses are at an infinite distance from each other, their gravitational potential energy is zero. When they are at a distance r from each,the gravitational PE is
PE=−Gmm_2r2
The minus sign-indicates that there is a distance in PE. This gives rise to an increase in kinetic energy. IF v1 and v2 are their distance r apart then, from the law of conservation of energy, we have
12m1v21=Gm1m2rorv1=√2Gm2r
and 12m2v22=Gm1m2rorv2=√2Gm1r
Therefore, their relative velocity if approach is
v1+v2=√2Gm2r+√2Gm1r=√2Gr(m1+m2)
=(2G(m1×m2)r)12
Topper's Solved these Questions
- BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)EXERCISE - Physics40videos
AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)
- BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)EXERCISE - Physics40videos
AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)
Similar Questions
N divisions on the main scale of a vernier calipers coincide with (N +1) division of the vernier scale. If each division of main scale is a units, then the least count of the calipers is :
04:14View SolutionA monoatomic ideal gas through a cyclic process as shown in the figure . The efficiency of this process is
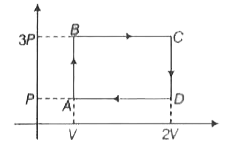 07:11View Solution
07:11View SolutionTwo objects of masses m and 4m are at rest at an infinite separation. They move towards each other under mutual gravitational attraction. If G is the universal gravitaitonal constant, then at separation r
08:14View SolutionTwo bodies of mass m_(1) and m_(2) are initially at rest placed infinite distance apart. They are then allowed to move towards each other under mutual gravitational attaction. Show that their relative velocity of approach at separation r betweeen them is v=sqrt(2G(m_(1)+m_(2)))/(r)
11:27View SolutionTwo particles m1 and m2 are initially at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when their separation is d.
08:22View SolutionTwo objectes of mass m and 4m are at rest at and infinite seperation. They move towards each other under mutual gravitational attraction. If G is the universal gravitational constant. Then at seperation r
03:17View SolutionTwo bodies of masses m1andm2 are initially at rest and infinite distance apart. Due to mutual attraction, they approach each other. When they are r distance apart, their relative velocity of approach is
View SolutionTwo bodies of masses m1 and m2 initially at rest at infinite distance apart move towards each other under gravitational force of attraction. Their relative velocity of approach when they are separated by a distance r is (G= universal gravitational constant.)
View SolutionTwo bodies of masses m1 and m2 are initially at rest a infinite distance apart. They are then allowed to move towards each other under mutual gravitaitonal attraction. Their relative velocity of approach at a separation distance r between them is
View SolutionTwo bodies of masses m1 and m2 are initially at rest at infinite distance aprat. They are then allowed to move towards each other under mutual gravitational attraction. Their relative velocity of approach at a separation distance r between them is
06:43View SolutionTwo bodies of masses m_(1)" and "m_(2) are initially at rest at infinite distance aprat. They are then allowed to move towards each other under mutual gravitational attraction. Their relative velocity of approach at a separation distance r between them is
View SolutionTwo objectes of mass m and 4m are at rest at and infinite seperation. They move towards each other under mutual gravitational attraction. If G is the universal gravitational constant. Then at seperation r
02:07View SolutionTwo bodies with masses M_1 and M_2 are initially at rest and a distance R apart. Then they move directly towards one another under the influence of their mutual gravitational attraction. What is the ratio of the distances travelled by M_1 to the distance travelled by M_2 ?
03:56View SolutionWrite an expression for the gravitational force of attraction between two bodies of masses m1 and m2 separated by a distance r .
06:08View SolutionTwo particles of masses m and M are initially at rest at an infinite distance apart. They move towards each other and gain speeds due to gravitational attraction. Find their speeds when the separation between the masses becomes equal to d.
03:22View Solution

