A solid sphere of 100 kg and radius 10 m moving in a space becomes a circular disc of radius 20 m in one hour. Then the rate of change of moment of inertia in the process is Solution in Telugu
Given, mass of solid sphere
radius of solid sphere
radius of circular disc
and time =1 hour=60 minute=
Moment of inertia of the solid sphere,
Similarly,
moment of inertia of the disc
Rate of change of moment of inertia
Topper's Solved these Questions
- AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)Book:TS EAMCET PREVIOUS YEAR PAPERSChapter:AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)Exercise:Physics
Explore 40 Videos
- AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)Book:TS EAMCET PREVIOUS YEAR PAPERSChapter:AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)Exercise:Physics
Explore 40 Videos
Similar Questions
N divisions on the main scale of a vernier calipers coincide with (N +1) division of the vernier scale. If each division of main scale is a units, then the least count of the calipers is :
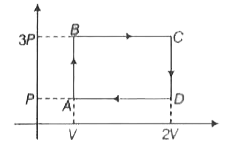
View SolutionA monoatomic ideal gas through a cyclic process as shown in the figure . The efficiency of this process is
View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
View Solutionद्रव्यमान M तथा त्रिज्या R के ठोस गोले का उसके व्यास के परितः जड़त्व-आघूर्ण है
View SolutionCalculate the moment of inertia of a solid sphere of mass 10 kg and radius 0.5 m, rotating about an axis 0.2 m from the centre of the sphere .
View SolutionA sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
View SolutionThe moment of inertia of a circular disc about its diameter is 500 kg m2. If its radius is 2 m, than its radius of gyration is
View SolutionWhat is the moment of Inertia of a sphere of mass 20 kg and radius 14 m about its diameter ?
View SolutionIf the radius of gyration of a solid disc of mass 10 kg about an axis is 0.40 m, then the moment of inertia of the disc about that axis is
View SolutionThe moment of inertia of a solid sphere of mass M and radius R about the tangent is
View SolutionThere is a solid sphere of mass m. Moment of inertia about the axis passing through the centre of sphere is I. If the material of the sphere is recast to a disc of same radius then what would be its moment of inertia?
View SolutionA solid sphere of mass M and radius R having moment of inertia I about its diameter is recast into a solid disc of radius r and thickness t. The moment of inertia of the disc about an axis about the edge and perpendicular to the plane is I. Then the radius r of the disc is given by :
View Solution20 किग्रा द्रव्यमान के एक ठोस बेलन की लम्बाई 1 मीटर तथा त्रिज्या 0.2 मीटर है जड़त्व आघूर्ण होगा:
View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
View Solution
