A semicircular plate of mass m has radius r and centre c. The centre of mass of the plate is at a distance x from its centre c. Its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane is Solution in Telugu
mr22
mr24
mr22+mx2
mr22−mx2
Given,
Mass of a semicircular plate=m
radius of semicircular plate=r
According to the question we can drawn the following diagram,
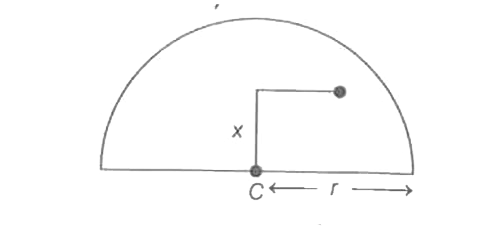
Now, from the parallel axis theorem,
Ic=Icm+mx2
Icm=Ic−mx2
Here, Ic=(mr)22
Hence, moment of inertia of semicircular plate about an axis passing through its centre of mass and perpendicular to it.s plane is
Icm=mr22−mx2
Topper's Solved these Questions
- AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)EXERCISE - Physics
40 Videos
- AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)EXERCISE - Physics
40 Videos
Similar Questions
N divisions on the main scale of a vernier calipers coincide with (N +1) division of the vernier scale. If each division of main scale is a units, then the least count of the calipers is :
View SolutionA monoatomic ideal gas through a cyclic process as shown in the figure . The efficiency of this process is
View SolutionMoment of inertia of a thin circular plate of mass M , radius R about an axis passing through its diameter is I . The moment of inertia of a circular ring of mass M , radius R about an axis perpendicular to its plane and passing through its centre is
View SolutionThe mass of a thin circular plate is M and its radius is R . About an axis in the plane of plate at a perpendicular distance R//2 from centre of plate, its moment of inertia is
View SolutionIf I moment of inertia of a thin circular plate about an axis passing through tangent of plate in its plane. The moment of inertia of same circular plate about an axis perpendicular to its plane and passing through its centre is
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr^(2)(-(k)/(pi^(2))) . Find the value of k.
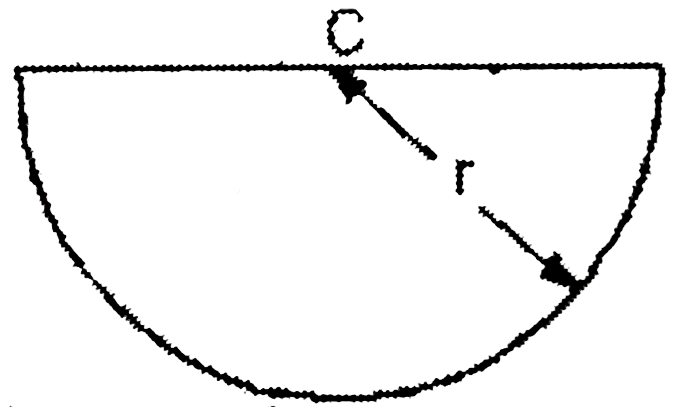
View SolutionA semicircular lamina of mass m and radius 'r' and centre C. Its center of mass is at a distance 'x' from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
View SolutionA thin wire of mass m and length l is bent in the form of a ring . Moment of inertia of that ring about an axis passing through its centre and perpendicular to its through its centre and perpendicular to its plane is
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionA thin disc of mass M and radius R has mass per unit area σ(r)=kx2 where r is the distance from its centre. Its moment of inertia about an axis going through its centre of mass and perpendicular to its plane is:
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionThe moment of inertia of a circular disc of mass m and radius r about an perpendicular axis passing through its centre is
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View Solution
