A ray of light is refracted through a transparent sphere of refractive from μ in such a way that the ray passes through the ends of two radii inclined at an angle θ with each other. If δ is the angle of deviation of the ray while passing through the sphere then prove that,
μ=cos12(θ−δ)cosθ2
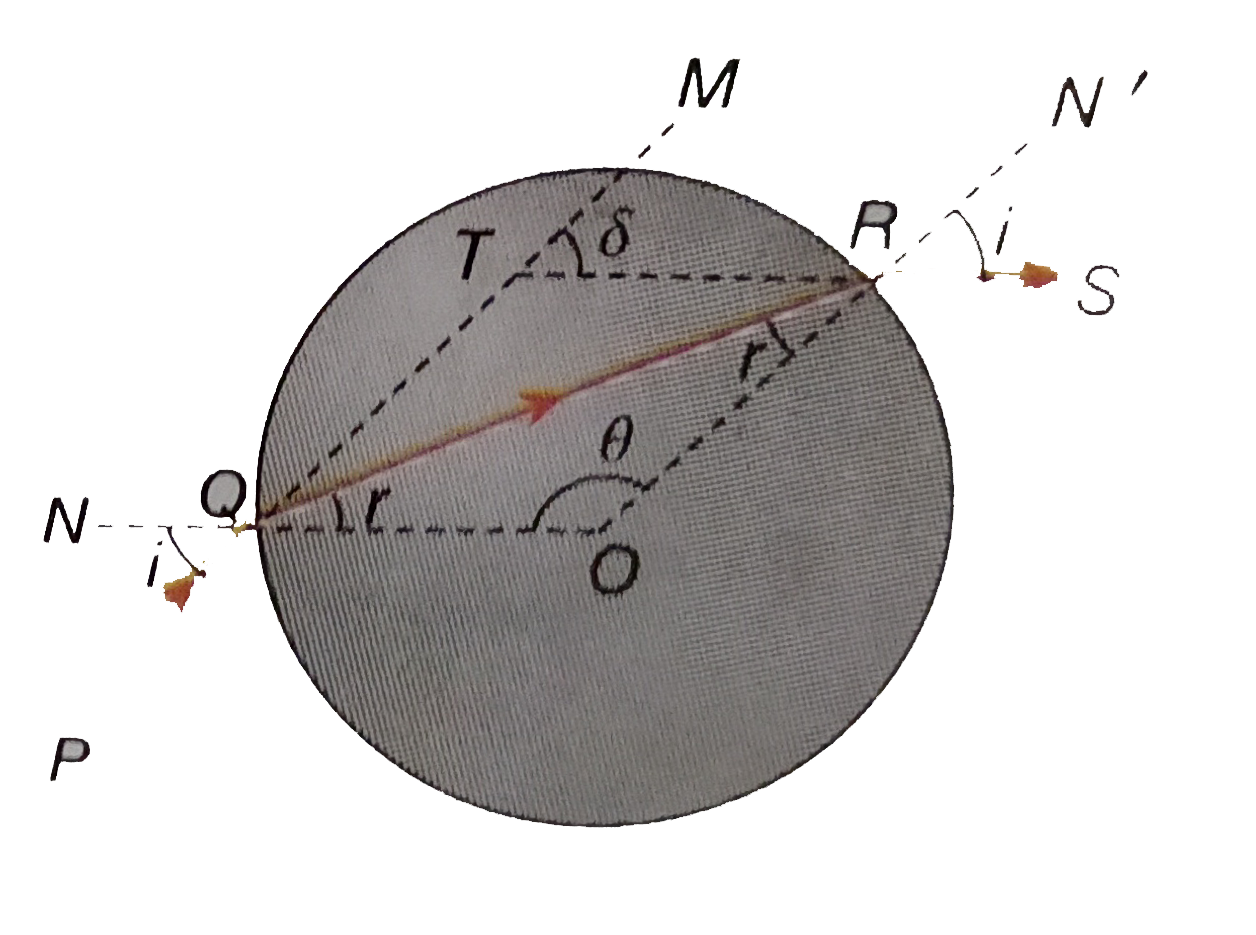
Let the ray PQ incident at Q on the sphere, is refracted along QR and emerges from the sphere along RS [Fig. 2.12]. Of the triangle OQR , OQ = OR (both are radii of the sphere).
∴ ∠OQR=∠ORQ
Let angle of incidence of the ray at Q=∠PQN=i and angle of refraction =∠OQR=r
So the angle of incidence of the ray at R is r and angle of refraction i.e. angle of emergence is i.
Angle of deviation of the incident ray,
δ=∠MTR=∠TQR+∠TRQ
=(i−r)+(i−r)=2(i−r)
From the triangle OQR we have, r+r+θ=180∘
or, 2r+θ=180∘or,r=90∘−θ2
From equation (1) we get, δ2=i−ror,i=δ2+r=δ2=90∘+δ2−θ2
Considering refraction at Q,
μ=sinisinr=sin(90∘+δ2−θ2)sin(90∘−θ2)
sin{90∘−12(θ−δ)}cos(θ)2=cos12(θ−δ)cos(θ)2
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING SKILL (HOTS QUESTION)
25 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION
18 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
A ray of light is refracted through a sphere whose material has a refractive index μ in such a way that it passes through the extremities of two radii which make an angle β with each other. Prove that if α is the deviation of the ray caused by its passage through the sphere, then
cos(β−α2)=μcos(βα)
View SolutionA ray of light is refracted through a sphere whose material has a refractive index μ in such a way that it passes through the extremities of two radii which make an angle β with each other. Prove that if α is the deviation of the ray caused by its passage through the sphere, then
cos(β−α2)=μcos(βα)
View Solution
Knowledge Check
The deviation δ of a ray on passing through a prism of small angle A is.
Aμ−1ABAμ−1C(μ−1)ADnone of theseThe angle of a prism is 60∘ and its refractive index is √2 . The angle of minimum deviation suffered by a ray of light in passing through it is
AAbout 20∘B30∘C60∘D45∘The angle of a prism is 60∘ and its refractive index is √2. The angle of minimum deviation suffered by a ray of light in passing through it is
AAbout 20∘B30∘C60∘D45∘
A ray of light passes through a transparent sphere of refractive index μ and radius R. If b is the distance between the incident ray and diameter of the sphere which is parallel to that ray, What is the value of the deviation?
View SolutionThe angle of a prism is 60∘ and its refractive index is √2. The angle of minumum deviation sufferred by a ray of light in passing through it is
View SolutionDefine refractive index of a transparent medium. A ray of light passes through a triangular prism. Plot a graph showing the variation of the angle of deviation with the angle of incidence.
View SolutionTwo plane mirrors are inclined to each other at an angle θ. A ray of light is reflected at one
mirror and then at the other. Find the total deviation of the ray.
View SolutionTwo plane mirrors are inclined to each other at an angle θ. A ray of light is reflected at one
mirror and then at the other. Find the total deviation of the ray.
View Solution
