A cube has refractive index μ1 . There is a plane of refractive index μ2(μ2<μ1) upon it. A ray travelling through air is incident on a side face of the cube. The refracted ray is incident on the upper face of the cube at the minimum angle for total internal reflection to occur. Finaily the reflected ray emerges from opposite face. Show that if the angle of emergence is ϕ then sinϕ=√μ21−μ22.
In Fig. 2.28, PQ = incident ray on the side face of the cube, QR = refracted ray inside the cube, RS = totally reflected ray from the upper face of the cube, ST = emergent ray from the opposite face. Let critical angle for total reflection be θc.
According to the question, θ.c≈θc
i.e. sinθ.c≈θc=12μ1=1μ1μ2=μ2μ1
Angle of incidence of the ray RS=i=90∘−θc and angle of refraction = ϕ.
∴ sinisinϕ = refractive index of air with respect to the cube
=1refractive index of the with respect to air
or. sinisinϕ=1μ1
or, sinϕ=μ1sini
=μ1sin(90∘−θc)=μ1cosθc
=μ1√1−sin2θc
=μ1
⎷1−μ22μ21=√μ21−μ22
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING SKILL (HOTS QUESTION)
25 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION
18 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
A light ray from air is incident on a glass plate of thickness t and refractive index μat an angle of incidence equal to the angle of total internal reflection of glass. Compute the displacement of the ray due to this plate in terms of thickness and refractive index of glass μ.
View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:
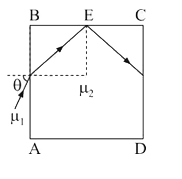
View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:

View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:

View SolutionThe refractive index of a prism is μ. Find the maximum angle of the prism for which a ray incident on it will be transmitted through other face without total internal reflection.
View SolutionThe refractive index of a prism is μ. Find the maximum angle of the prism for which a ray incident on it will be transmitted through other face without total internal reflection.
View SolutionRefractive index of the material of concave lens is μ. The lens is immersed inb a medium of refractive index μ1(μ1>μ). A parallel beam of light is incident on the lens. Draw a diagram to show the path of emergent rays.
View SolutionThe refractive index of the core of an optical fibre is μ2 and that of the cladding is μ1 .The angle of incidence on the face of the core so that the light ray just under goes total internal reflection at the cladding is
View SolutionThe refractive index of the core of an optical fibre is μ2 and that of the cladding is μ1. The angle of incidence on the face of the core of that the light ray just under goes total internal reflection at the cladding is
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View Solution
