The refractive index of a prism is μ. Find the maximum angle of the prism for which a ray incident on it will be transmitted through other face without total internal reflection.
The correct Answer is:2 sin^(-1) ((1)/(mu))
To find the maximum angle of a prism for which a ray incident on it will be transmitted through the other face without total internal reflection (TIR), we can follow these steps:
Step 1: Understand the Conditions for Total Internal Reflection
Total internal reflection occurs when the angle of incidence in a denser medium exceeds the critical angle. For a ray to pass through the prism without TIR, the angle of refraction at the second face of the prism must be less than the critical angle.
Step 2: Define the Angles
Let:
- A = angle of the prism
- I = angle of incidence at the first face
- R = angle of refraction at the first face
- R′ = angle of incidence at the second face
- μ = refractive index of the prism
Step 3: Apply Snell's Law
At the first face of the prism, we apply Snell's law:
n1sinI=n2sinR
Assuming the light is coming from air (where n1=1) into the prism (where n2=μ):
sinI=μsinR(1)
Step 4: Relate Angles of Refraction and Incidence
From the geometry of the prism, we know:
R+R′=A(2)
Where R′ is the angle of incidence at the second face.
Step 5: Condition for No Total Internal Reflection
For no total internal reflection at the second face, the angle of incidence R′ must be less than the critical angle IC. The critical angle can be defined as:
IC=sin−1(1μ)
Thus, we have:
R′<IC(3)
Step 6: Substitute and Rearrange
From equation (2), we can express R′ in terms of R:
R′=A−R
Substituting this into inequality (3):
A−R<sin−1(1μ)
Rearranging gives:
A<R+sin−1(1μ)(4)
Step 7: Use Snell's Law Again
From equation (1), we can express R in terms of I:
R=sin−1(sinIμ)
To find the maximum angle A, we need to maximize R. The maximum occurs when I approaches 90∘:
R→sin−1(1μ)
Step 8: Final Expression for Maximum Angle
Substituting this back into equation (4):
A<sin−1(1μ)+sin−1(1μ)
Thus, the maximum angle Amax is:
Amax=2sin−1(1μ)
Conclusion
The maximum angle of the prism for which a ray incident on it will be transmitted through the other face without total internal reflection is:
Amax=2sin−1(1μ)
---
Total internal reflection occurs when the angle of incidence in a denser medium exceeds the critical angle. For a ray to pass through the prism without TIR, the angle of refraction at the second face of the prism must be less than the critical angle.
Let:
- A = angle of the prism
- I = angle of incidence at the first face
- R = angle of refraction at the first face
- R′ = angle of incidence at the second face
- μ = refractive index of the prism
At the first face of the prism, we apply Snell's law:
n1sinI=n2sinR
Assuming the light is coming from air (where n1=1) into the prism (where n2=μ):
sinI=μsinR(1)
From the geometry of the prism, we know:
R+R′=A(2)
Where R′ is the angle of incidence at the second face.
For no total internal reflection at the second face, the angle of incidence R′ must be less than the critical angle IC. The critical angle can be defined as:
IC=sin−1(1μ)
Thus, we have:
R′<IC(3)
From equation (2), we can express R′ in terms of R:
R′=A−R
Substituting this into inequality (3):
A−R<sin−1(1μ)
Rearranging gives:
A<R+sin−1(1μ)(4)
From equation (1), we can express R in terms of I:
R=sin−1(sinIμ)
To find the maximum angle A, we need to maximize R. The maximum occurs when I approaches 90∘:
R→sin−1(1μ)
Substituting this back into equation (4):
A<sin−1(1μ)+sin−1(1μ)
Thus, the maximum angle Amax is:
Amax=2sin−1(1μ)
The maximum angle of the prism for which a ray incident on it will be transmitted through the other face without total internal reflection is:
Amax=2sin−1(1μ)
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-262videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-380videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Problem33videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS16videos
GRAVITATION
Similar Questions
The refractive index of a prism is 2. this prism can have a maximum refracting angle of
View SolutionRefractive index of a prism is √7/3 and the angle of prism is 60∘. The minimum angle of incidence of a ray that will be transmitted through the prism is
View SolutionRefractive index of a prism is √73 and the angle of prism is 60∘. The limiting angle of incidence of a ray that will be transmitted through the prism is approximately
View SolutionMonochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ, a ray, incident at an angle θ, on the face AB would get transmitted through the face AC of the prism provided:
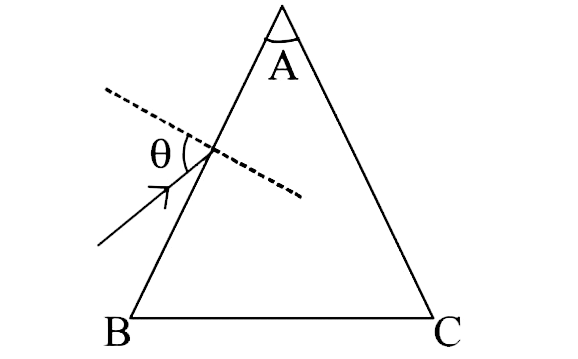 View Solution
View SolutionThe refractive index of the material of a prism is √2 and the angle of the prism is 30∘. One of the two refracting surfaces of the prism is made a mirror inwards, by silver coating. A beam of monochromatic light entering the prism from the other face will retrace its path (after reflection from the silvered surface) if its angle of incidence on the prism is
View SolutionACB is right-angled prism with other angles as 60∘ and 30∘ . Refractive index of the prism is 1.5. AB has thin layer of liquid on it as shown. Light falls normally on the face Ac. For total internal reflection, maximum refractive index of the liquid is
 View Solution
View SolutionLight is incident normally on face AB of a prism as shown in Figure. A liquid of refractive index μ is placed on face AC of the prism. The prism is made of glass of refractive indes 3/2 . Find the limits of μ for which total internal reflection takes place on the face AC.
(A)μ>√32 (B)3√34>μ (C)μ>√3 (D)μ<√32 View Solution
View SolutionThe refractive index of the core of an optical fibre is μ2 and that of the cladding is μ1. The angle of incidence on the face of the core of that the light ray just under goes total internal reflection at the cladding is
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
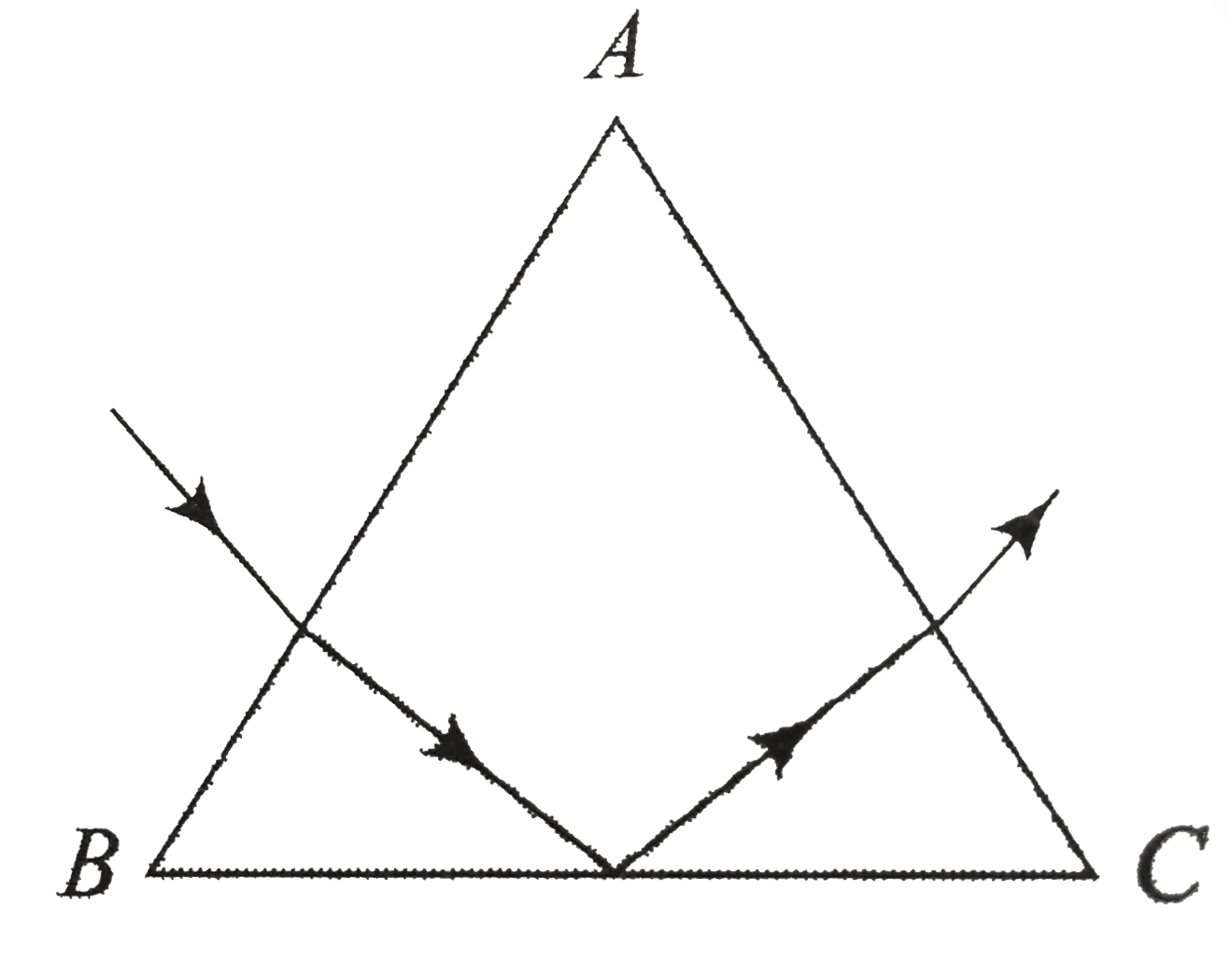 View Solution
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
View Solution

