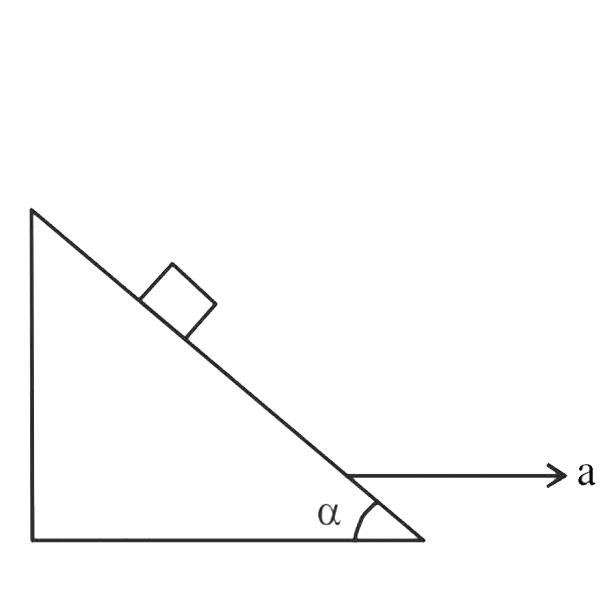
A block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and θ for the block to remain stationary on the wadge is

a = g cos θ
a = gsinθ
a = gcosecθ
a = g tanθ
For the mass m to remain still in the non-inertial reference frame,
Rsinθ = ma …(1)
Rcosθ = mg …(2)
(1) ÷ (2) we get,
tanθ=ag or,a=gtanθ
The option D is correct.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - CBSE SCANNER
24 Videos
- NEWTON'S LAWS OF MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - EXAMINATION ARCHIVE WITH SOLUTIONS (AIPMT)
3 Videos
- NATURE OF VIBRATIONBOOK - CHHAYA PUBLICATIONCHAPTER - NATURE OF VIBRATIONEXERCISE - EXERCISE (CBSE SCANNER)
2 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - CBSE SCANNER
19 Videos
Similar Questions
A block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution
Knowledge Check
A block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
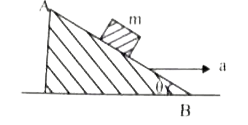 Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθA block of mass m resting on a wedge of angle θ as shown in the figure. The wedge is given an acceleration a. What is the minimum value of a so that the mass m falls freely ?
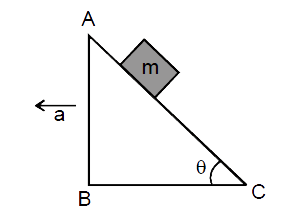 AgBgcosθCgcotθDgtanθ
AgBgcosθCgcotθDgtanθA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθ
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
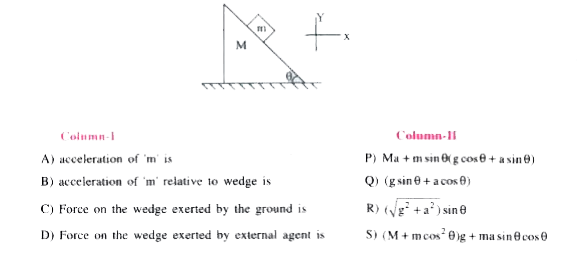
View SolutionA smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is

View SolutionA block is kept on a frictionless inclined surface with angle of inclination α. The incline is given an acceleration 'a' to keep the block stationary. Then a is equal to
View SolutionA block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
View Solution
