The angle of inclination of a plane is 30∘ with the horizontal. A uniform circular disc of mass m and radius R is rolling up the plane. If coefficients of both static and sliding friction are μ and only frictional and gravitational forces are effective what is the force of friction acting on the disc and what is its direction along the inclined plane?
The correct Answer is:mg2,upwards
Topper's Solved these Questions
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - ENTRANCE CORNER (Assertion-reason type )
7 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - ENTRANCE CORNER ( Multiple correct answers type )
3 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - Hots Numerical Problems ( Based on Fundamentals of Friction )
1 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - CBSE SCANNER
18 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - CBSE SCANNER
1 Videos
Similar Questions
A uniform disc of mass m and radius R is rolling up a rough inclined plane which makes an angle of 30∘ with the horizontal. If the coefficients of static and kinetic friction are each equal to μ and the only force acting are gravitational and frictional, then the magnitude of the frictional force acting on the disc is and its direction is .(write up or down) the inclined plane.
View SolutionA uniform disc of mass m and radius R is rolling up a rough inclined plane which makes an angle of 30∘ with the horizontal. If the coefficients of static and kinetic friction are each equal to μ and the only force acting are gravitational and frictional, then the magnitude of the frictional force acting on the disc is and its direction is .(write up or down) the inclined plane.
View Solution
Knowledge Check
A block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
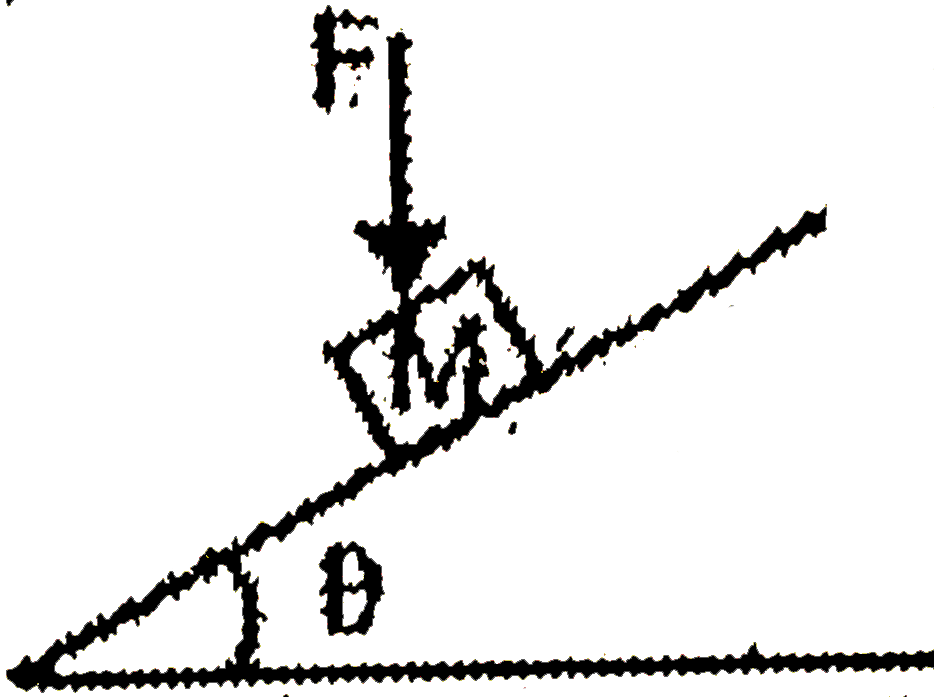 A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθA disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
A76B54C32Ddepends on angle of inclinationA block of mass m is at rest on an inclined plane. The coefficient of static friction is μ. The maximum angle of incline before the block begins to slide down is :
Atan−1(μ/m)Btan−1(μ)Ctan−1(μ/2)Dcos−1(μ)
A disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
View SolutionA spherical shell of mass m and radius R is rolling up without slipping on a rough inclined plane as shown in the figure. The direction of static friction acting on the shell is
View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View Solution
