In a hollow sphere the maximum height with respect to the lowest point at which a particle remains in equilibrium, is one-tenth of the radius of the sphere. What is the coefficient of friction between the sphere and the particle?
The correct Answer is:0.484
Topper's Solved these Questions
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - ENTRANCE CORNER (Assertion-reason type )
7 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - ENTRANCE CORNER ( Multiple correct answers type )
3 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - Hots Numerical Problems ( Based on Fundamentals of Friction )
1 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - CBSE SCANNER
18 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - CBSE SCANNER
1 Videos
Similar Questions
A cylinder and a hollow sphere are placed on a surface. If the height of the cylinder is equal to the diameter of the sphere, what is the ratio of the heights of centre of gravity of the cylinder and the sphere from the surfaced?
View SolutionDetermine the maximum horizontal force F that may be applied to the plank of mass m for which the solid sphere does not slip as it begins to roll on the plank. The sphere has a mass M and radius R. The coefficient of static and kinetic friction between the sphere and the plank are μsandμk respectively.
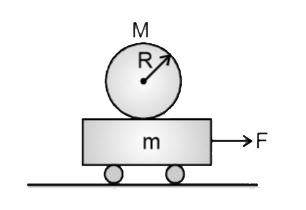
View Solution
Knowledge Check
Two identical heavy spheres of equal mass are placed on a smooth cup of radius 3 r where r is radius of each sphere.Then the ratio of reaction force between cup and any sphere to reaction force between two sphere is
A1B2C3D4A hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
AFriction opposes its translationBFriction supports rotation motionCOn decreasing θ, frictional force decreasesDAll of these
A sphere of radius R is supported by a rope attached to the wall. The rope makes an angle θ=45∘ with respect to the wall. The point where the rope is attached to the wall is at a distance of 3R2 from the point where the sphere touches the wall. Find the minimum coefficient of friction (μ) between the wall and the sphere for this equilibrium to be possible.
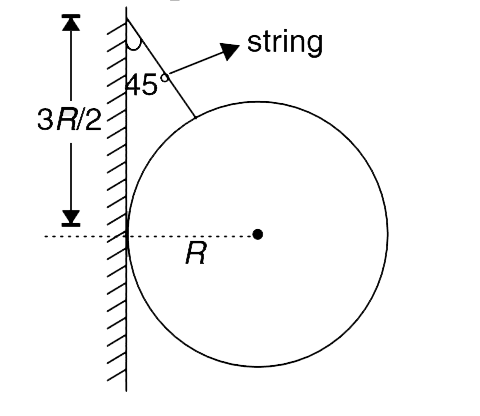
View Solution
Determine the maximum horizontal force F that may be applied to the plank of mass m for which the solid sphere does not slip as it begins to roll on the plank. The sphere has a mass M and radius R. The coefficient of static and kinetic friction between the sphere and the plank are μS and μk respectively.
View SolutionA sphere is placed in an inverted hollow conical vessel of base radius 5cm and vertical height 12cm. If the highest point of the sphere is at the level of the base of the cone, find the radius of the sphere. Show that the volume of the sphere and the conical vessel are as 40: 81.
View SolutionA uniform solid sphere of mass 1kg and radius 10 cm is kept stationary on a rough inclined plane by fixing a highly dense particle at B. Incination of plane is 37∘ with horizontal and AB is the diameter of the sphere which is parallel to the plane, as show in figure. Calculate
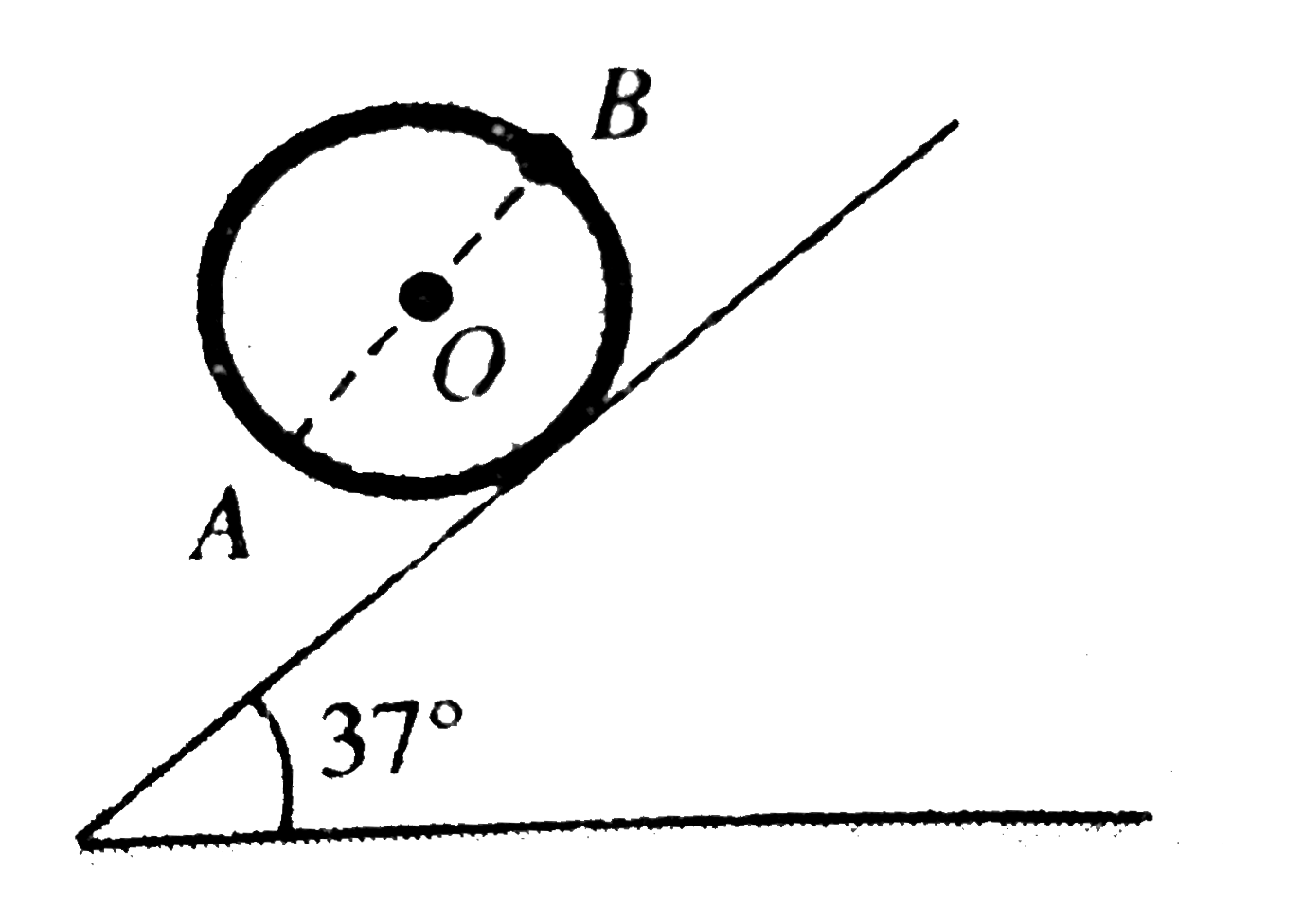
a. mass of the particle fixed at B
b. minimum required coefficient of friction between sphere and plane to keep sphere in equilibrium.
View SolutionA uniform solid sphere of mass 1kg and radius 10 cm is kept stationary on a rough inclined plane by fixing a highly dense particle at B. Incination of plane is 37∘ with horizontal and AB is the diameter of the sphere which is parallel to the plane, as show in figure. Calculate

a. mass of the particle fixed at B
b. minimum required coefficient of friction between sphere and plane to keep sphere in equilibrium.
View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View Solution
