A rod of length L and mass M is attached with a hinge on a wall at a point O. After releasing the rod from its vertical position OA, when it comes to the position OA', then what is the reaction on the point O of the rod by the hinge ?

Let the angular velocity of the rod at the horizontal position OA. is ω.
∴ At that instant its kinetic energy
=12Iω2=12.ML23.ω2=ML2ω26
The centre of mass of the rod shift down by L2 from OA to .OA. So, decrease in potential energy of the rod MgL2
According to the kinetic eneragy conservation law,
Mg12=ML2ω26or,ω=√3gL ⋯(1)
Two forces act on the rod at position OA. - (i) gravitational force (Mg) vertically downward direction and (ii) reaction force (n) of the hinge. Let the horizontal and the vertical components of n are nx and ny respectively, the horizontal and the vertical components of the acceleration of the centre of mass of the rod are ax and ay respectively.
∴ According to Fig.
Mg−ny=May ⋯(2)
and nx=Max=Mω2.L2[∵ax= centripetal acceleration ]
M.3gL.L2=32Mg
[ putting the value of ω from equation (1)]
The rod starts to rotate due to the action of torque created by ny and Mg.
If the angular acceleration of the rod is α,
Mg.L2=Iα=ML23α
∴ α=3g2L
∴ The acceleration along the vertical direaction,
ay=L2α=3g4
Putting the value of ay in equation (2) we get,
Mg−ny=3Mg4or,ny=Mg4
∴ n=√n2x+n2y=√(32Mg)2+(Mg4)2=√374Mg

Topper's Solved these Questions
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - Section Related Question
2 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
20 Videos
- QUESTION PAPERS OF WBCHSE -2018BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
Similar Questions
A rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View Solution
Knowledge Check
A uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:

The acceleration of the centre of mass of the rod isA−6g7ˆi−12g7ˆjB−12g7ˆi−6g7ˆjC−3g7ˆi−9g7ˆjD−9g7ˆi−3g7ˆjA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
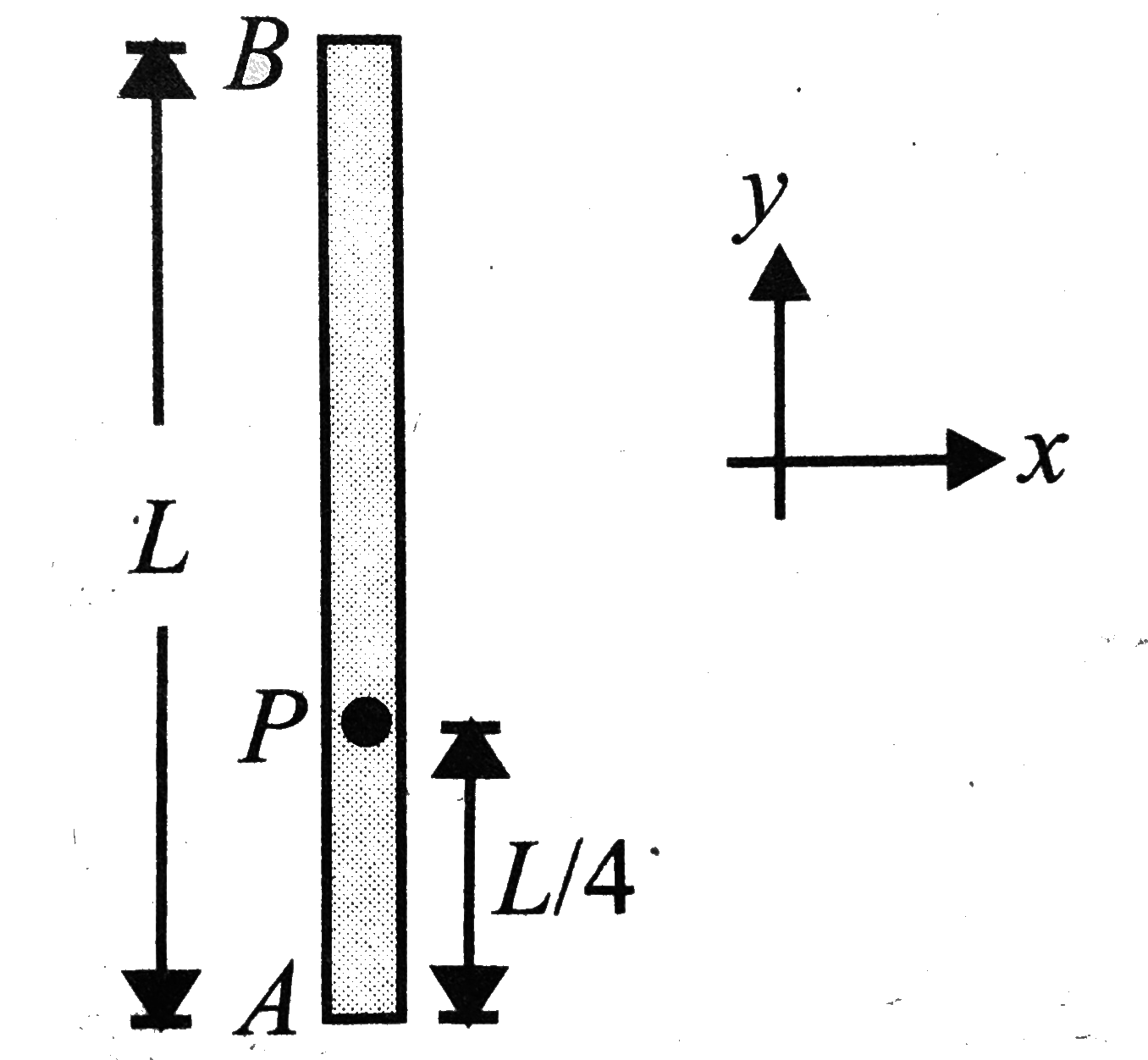
The acceleration of end B of the rod isA−6g7ˆi−12g7ˆjB−5g7ˆi−6g7ˆjC−18g7ˆi−5g7ˆjD−18g7ˆi−9g7ˆjA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
A32mgB2mgC52mgD3mg
A uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:

The acceleration of the centre of mass of the rod is
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:

The acceleration of end B of the rod is
View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
View SolutionA uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
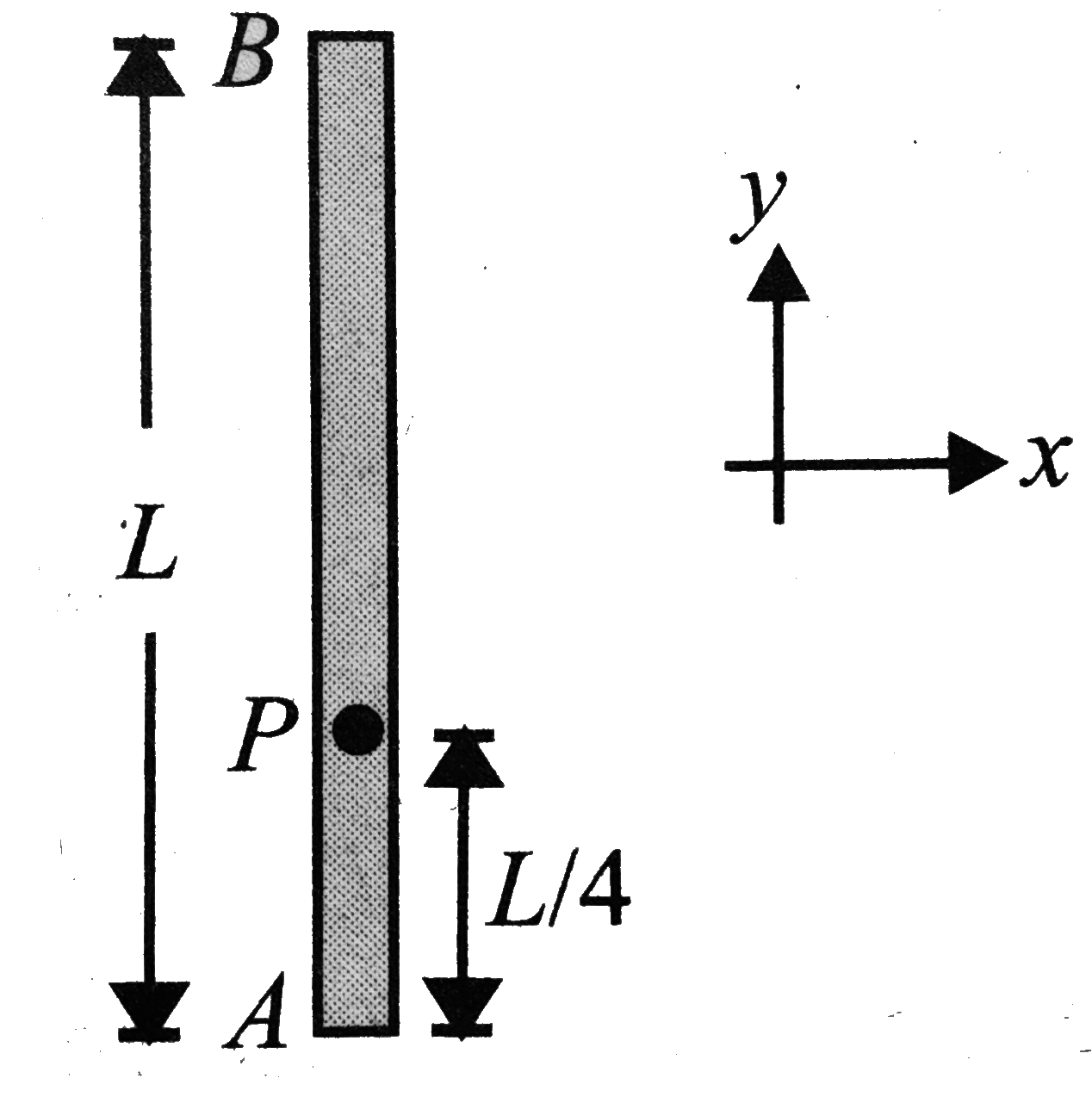
The reaction at hinge P is
View Solution
