A mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to a string which passes through a smooth hole in the plane as shown.
the tension in te string is increased gradually and finally m moves in circle of radius R02 . The final value of the kinetic energy is

mv20
14mv20
2mv20
12mv20
The correct Answer is:C
The torque acting on the moving mass is directed upward. The increasing tension in the string does not have any effect on the torque.
As a result, angular momentum will remain conserved,
i.e., mv0R0=mvR02 or,v=2v0
Hence, kinetic energy =12m(2v0)2=2mv20
Topper's Solved these Questions
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXAMINATION ARCHIVE with solutions (NEET )
8 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - CBSE SCANNER
10 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXAMINATION ARCHIVE with solutions (JEE Main )
10 Videos
- QUESTION PAPERS OF WBCHSE -2018BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
Similar Questions
A mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0, The mass is attached to a string which passes through a smooth hole in the plane as shown.
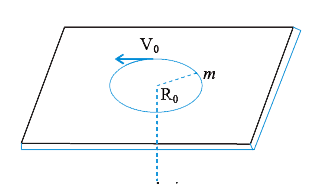
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy is :
View SolutionA mass m moves in a circles on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to string which passes through a smooth hole in the plane as shown.
The tension in string is increased gradually and finally m moves in a circle of radius R02. the final value of the kinetic energy is
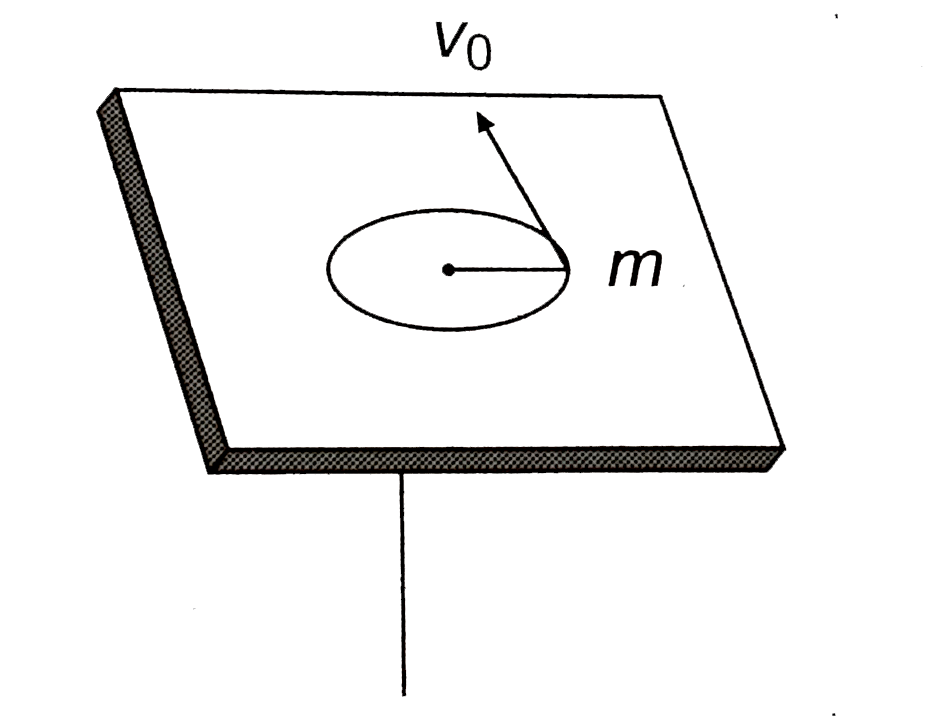
View Solution
Knowledge Check
A mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to a string which passes through a smooth hole in the plane as shown.
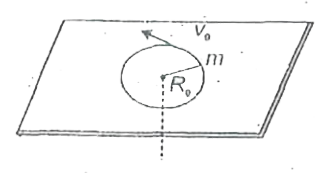
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy isA12mv20Bmv20C14mv20D2mv20A mass m moves in a circles on a smooth horizontal plane with velocity v0 at a radius R0. The mass is atteched to string which passes through a smooth hole in the plane as shown.
The tension in string is increased gradually and finally m moves in a cricle of radius R02. the final value of the kinetic energy is
 A14mv02B2mv20C12mv02Dm20
A14mv02B2mv20C12mv02Dm20A block of mass m is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block
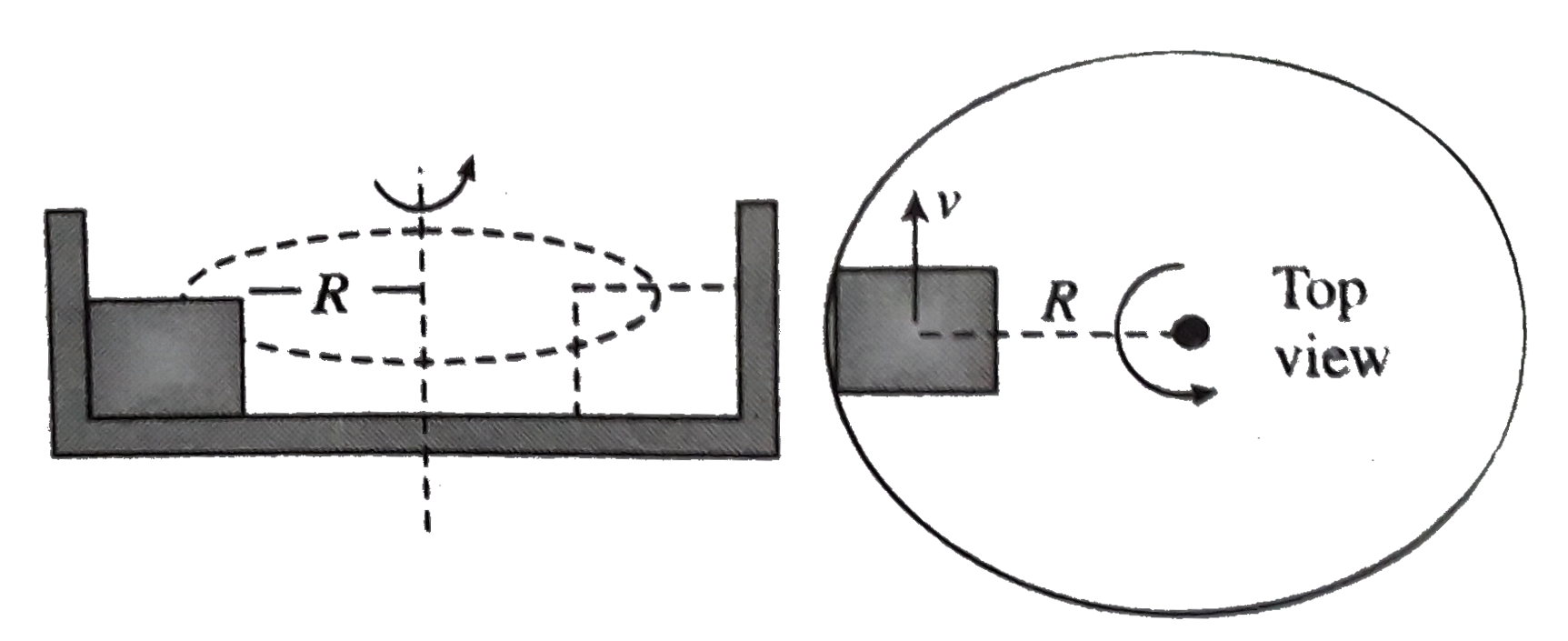 Amv2RBmgCm√v4R2+4g2Dm√v4R2+g2
Amv2RBmgCm√v4R2+4g2Dm√v4R2+g2
A mass m moves in a circles on a smooth horizontal plane with velocity v0 at a radius R0. The mass is atteched to string which passes through a smooth hole in the plane as shown.
The tension in string is increased gradually and finally m moves in a cricle of radius R02. the final value of the kinetic energy is

View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png)
View SolutionTwo masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is

View SolutionA block of mass m is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block

View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View Solution
