Assuming the earth's orbit around the sun to be circular, show that the area swept by its radius vector in unit time (areal velocity of the earth) is a constant.
Suppose the earth moves in a circular orbit of radius r with the sun at the centre (O) of the orbit [Fig. 1.5].

Let the radius vector OP , in an infinitesimal interval of time dt, describe an angle at the centre. Hence are PQ =. As value of PQ is very small, the arc PQ can be taken to be a straight line (chord PQ).
Area swept in time dt =area of triangle OPQ
Area swept per unit time = constant [as orbit is circular, r and of the earth should be constants]
Area swept in unit time by the radius vector of the earth is a constant.
Topper's Solved these Questions
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - SECTION RELATED QUESTIONS
18 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
41 Videos
- NEWTON'S LAWS OF MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - CBSE SCANNER
24 Videos
- ONE - DIMENSIONAL MOTION BOOK - CHHAYA PUBLICATIONCHAPTER - ONE - DIMENSIONAL MOTION EXERCISE - CBSE SCANNER
19 Videos
Similar Questions
Knowledge Check
Assume the earth's orbit around the sun as circular and the distance between their centres as D Mass of the earth is M and its radius is R if earth has an angular velocity ω0 with respect to its centre and ω with respect to the centre of the sun, the total kinetic energy of the earth is:
AMR2ω205[1+(ω(ω0)2+52)Dω(Rω0)2]BMR2ω205[1+52(DωRω0)2]C52MR2ω20[1+52(DωRω0)2]D25MR2ω20[1+(ωω0)2+52(DωRω0)2]A planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:
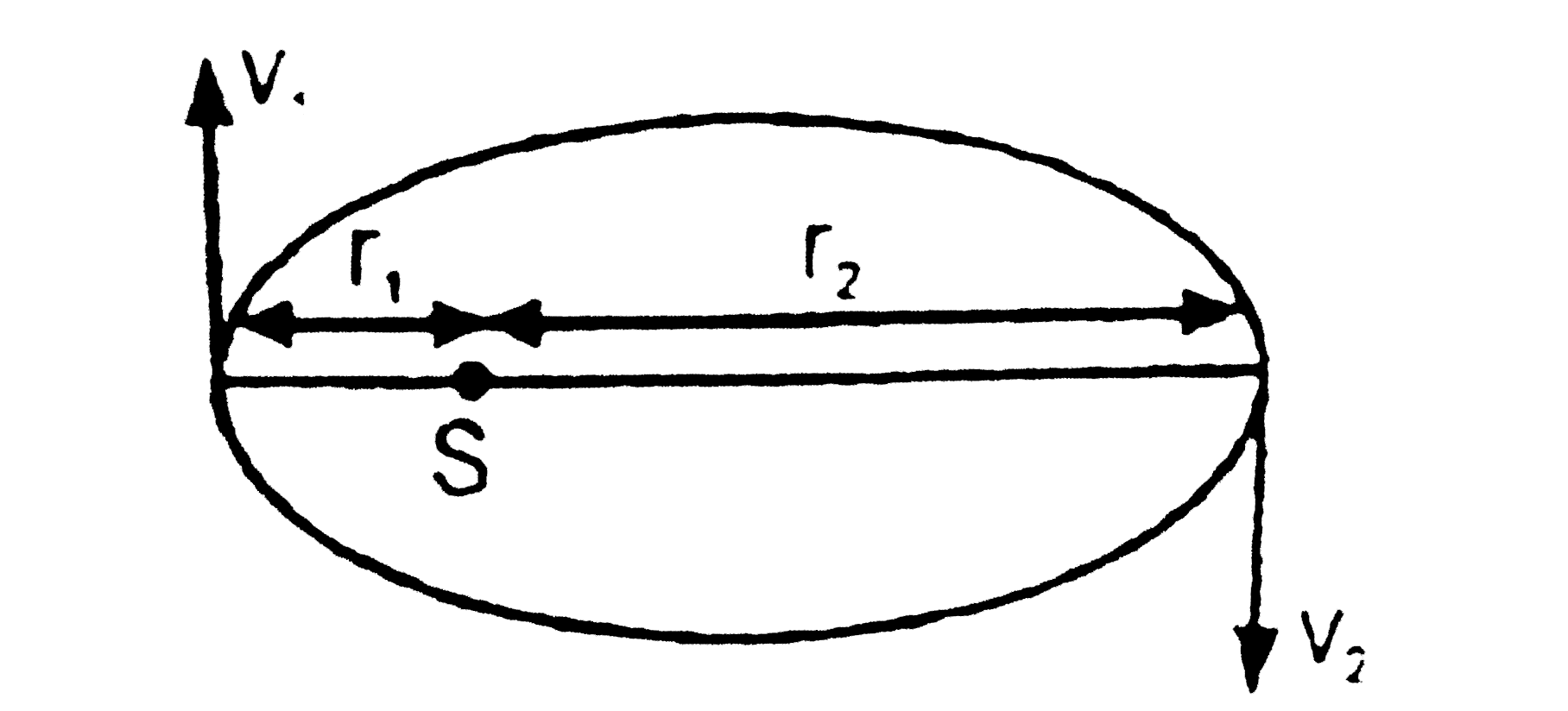 A14r2v2B12v1v1C12v1r21r2Ddependent on the position of planet from sun
A14r2v2B12v1v1C12v1r21r2Ddependent on the position of planet from sunAssuming that earth and mars move in circular orbits around the sun, with the martian orbit being 1.52 times the orbital radius of the earth. The length of the martian year is days is
A(1.52)2/3×365B(1.52)3/2×365C(1.52)2×365D(1.52)3×365
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 km/s
View SolutionA planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:

View SolutionThe earth, moving around the sun in a circular orbit, is acted upon by a force and hence work must be done on earth by this force.
View SolutionThe earth, moving around the sun in a circular orbit, is acted upon by a force and hence work must be done on earth by this force.
View SolutionAssuming that earth and mars move in circular orbits around the sun, with the martian orbit being 1.52 times the orbital radius of the earth. The length of the martian year is days is
View Solution
