From a solid sphere of mass M and radius R, a spherical portion of radius R2 is removed as shown in the figure. Taking gravitational potential V=0 at r=∞, the potential at the centre of the cavity thus formed is (G=gravitational constant)

−GM2R
−GMR
−2GM3R
−2GMR
The correct Answer is:B
Potential of a solid sphere of mass m and radius r at a distance
x(x<r)=Gm2r3(3r2−x2).
Here the combination of a solid sphere of mass M and radius R with another solid sphere of mass −M8and radius R2 can be considered as the final system. The centre of the hollow sphere is situated at a distance of x=R2 from the centre of the solid sphere. Now potential at that point due to the solid sphere,
V1=−GM2R3[3R2−(R2)2]=−GM2R3⋅114R2=−118GMR
At the centre of the hollow sphere for the sphere x=0 So, potential at that point,
V2=−G×(−M/8)2(R2)3[3(R2)2−0]
=GM2R3⋅34R2=38GMR
∴V=V1+V2=−118GMR+38GMR=−GMR
Topper's Solved these Questions
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - EXAMINATION ARCHIVE WITH SOLUTIONS (AIPMT)
3 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - EXAMINATION ARCHIVE WITH SOLUTIONS (NEET)
6 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - EXAMINATION ARCHIVE WITH SOLUTIONS (WBJEE)
4 Videos
- NEWTON'S LAWS OF MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - CBSE SCANNER
24 Videos
- ONE - DIMENSIONAL MOTION BOOK - CHHAYA PUBLICATIONCHAPTER - ONE - DIMENSIONAL MOTION EXERCISE - CBSE SCANNER
19 Videos
Similar Questions
From a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown
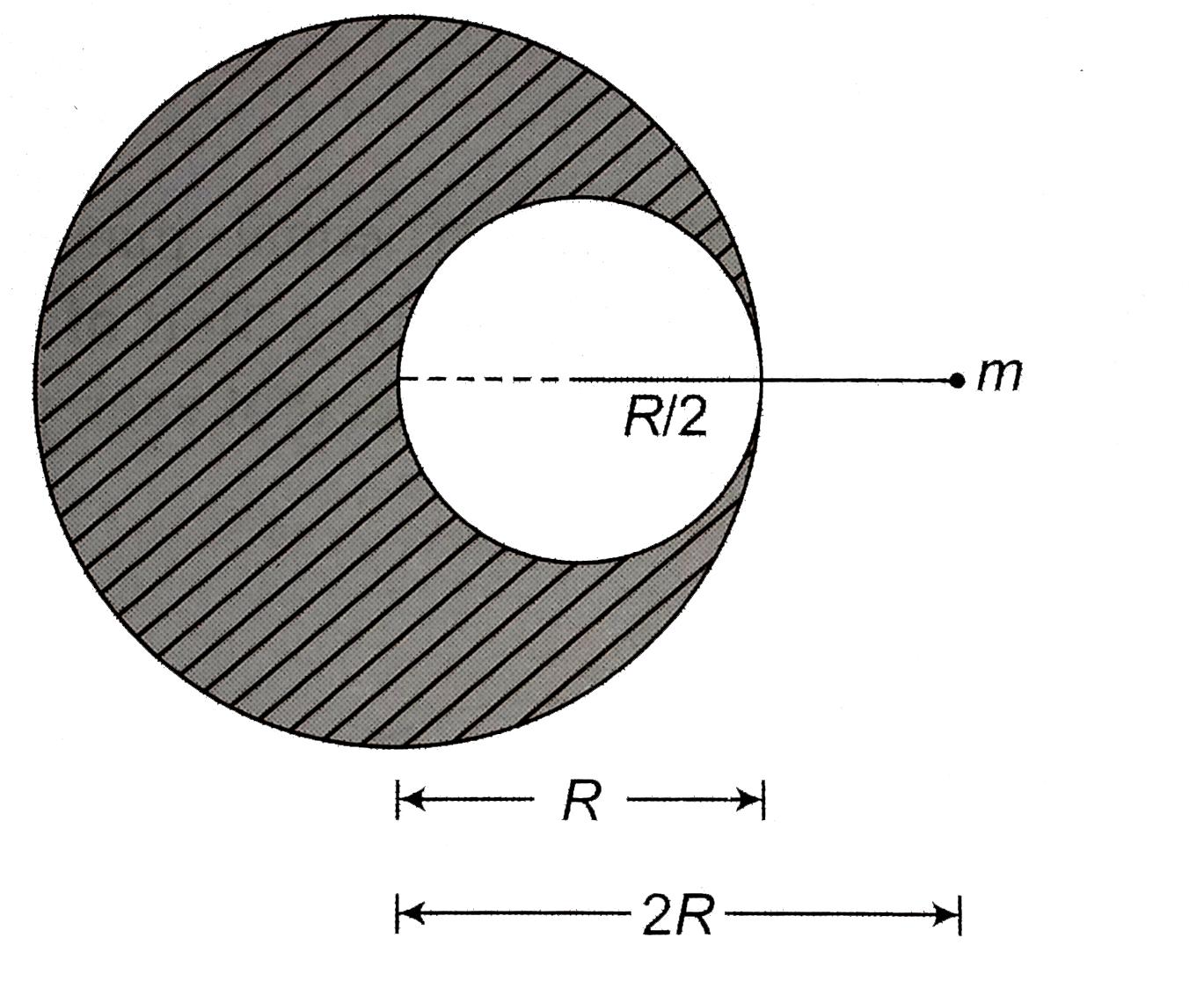
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution
Knowledge Check
From a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V=0atr=∞, the potential at (G = gravitational constatn)
 A−2GM3RB−2GMRC−GM2RD−GMR
A−2GM3RB−2GMRC−GM2RD−GMRFrom a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V=0atr=∞, the potential at (G = gravitational constatn)
 A−2GM3RB−2GMRC−GM2RD−GMR
A−2GM3RB−2GMRC−GM2RD−GMRTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
A−GMrB−2GmrC−GM2rD−4GMr
A sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
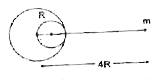
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ

View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View Solution
