The correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
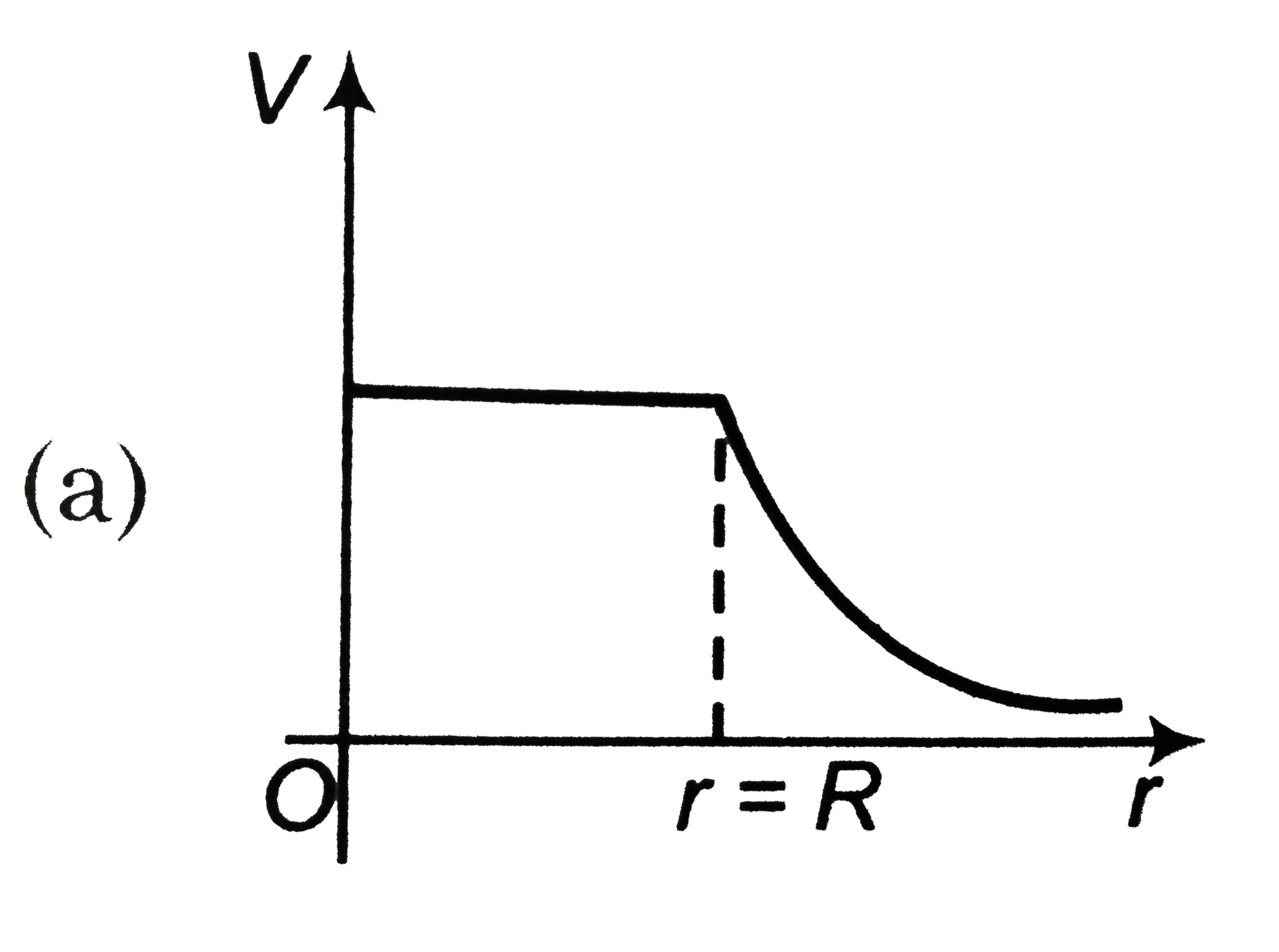
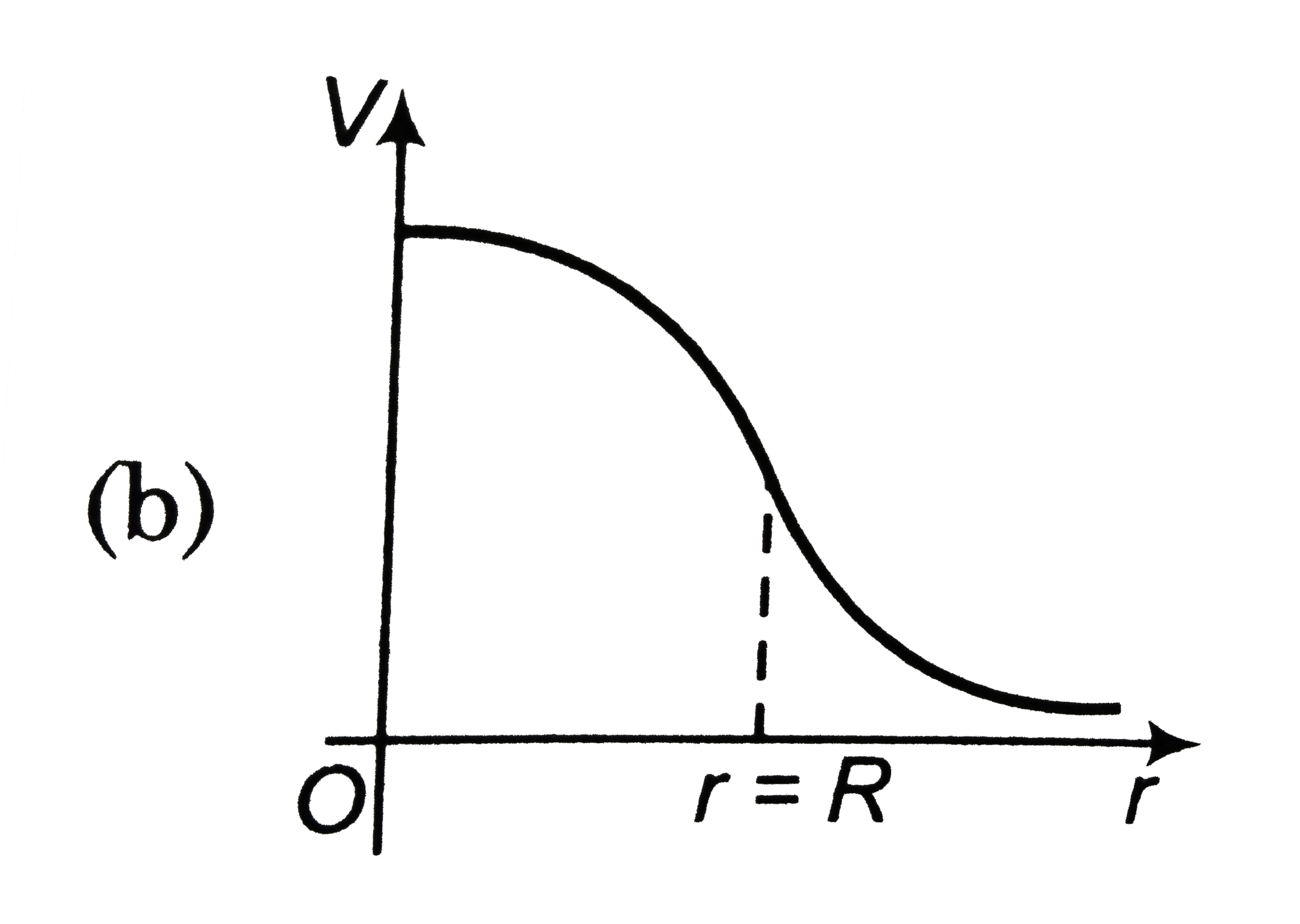
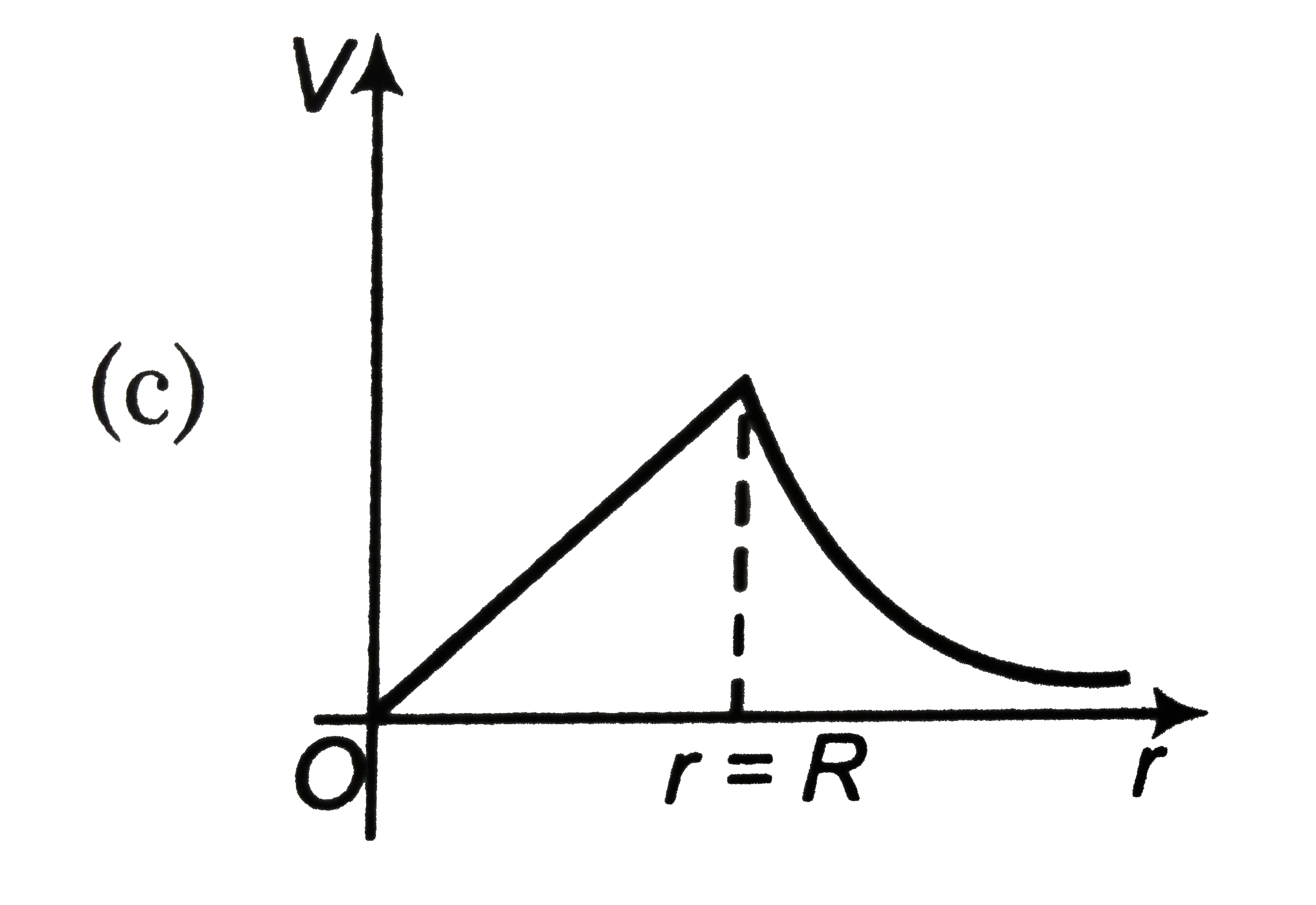
None of these
The correct Answer is:D
To solve the question regarding the variation of gravitational potential V with radius r measured from the center of the Earth, we can follow these steps:
1. Understanding Gravitational Potential:
The gravitational potential V at a distance r from the center of a solid sphere (like Earth) is given by the formula:
V=−GMr
for r≥R (outside the sphere), where G is the gravitational constant and M is the mass of the Earth.
2. Potential Inside the Sphere:
For points inside the sphere (where r<R), the gravitational potential is constant and given by:
V=−3GM2R
This means that as we move from the center of the Earth to the surface, the potential does not change.
3. At the Surface of the Earth:
At the surface of the Earth (where r=R), we can substitute r in the formula for outside the sphere:
V=−GMR
4. Graphical Representation:
- For r<R: The gravitational potential remains constant at −3GM2R.
- For r=R: The potential changes to −GMR.
- For r>R: The potential decreases as −GMr.
5. Conclusion:
The variation of gravitational potential V with radius r can be summarized as:
- Constant value of V=−3GM2R for r<R.
- V decreases as r increases for r≥R.
Final Answer:
The correct variation of gravitational potential V with radius r measured from the center of the Earth is that it remains constant for r<R and decreases as −GMr for r≥R. Since all options provided are in the positive axis, the answer is "none of these".
The gravitational potential V at a distance r from the center of a solid sphere (like Earth) is given by the formula:
V=−GMr
for r≥R (outside the sphere), where G is the gravitational constant and M is the mass of the Earth.
For points inside the sphere (where r<R), the gravitational potential is constant and given by:
V=−3GM2R
This means that as we move from the center of the Earth to the surface, the potential does not change.
At the surface of the Earth (where r=R), we can substitute r in the formula for outside the sphere:
V=−GMR
- For r<R: The gravitational potential remains constant at −3GM2R.
- For r=R: The potential changes to −GMR.
- For r>R: The potential decreases as −GMr.
The variation of gravitational potential V with radius r can be summarized as:
- Constant value of V=−3GM2R for r<R.
- V decreases as r increases for r≥R.
The correct variation of gravitational potential V with radius r measured from the center of the Earth is that it remains constant for r<R and decreases as −GMr for r≥R. Since all options provided are in the positive axis, the answer is "none of these".
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Level 1 Subjective
Explore 19 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Level 2 Single Correct
Explore 22 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Level 1 Assertion And Reason
Explore 11 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
Knowledge Check
Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).
A B
B C
C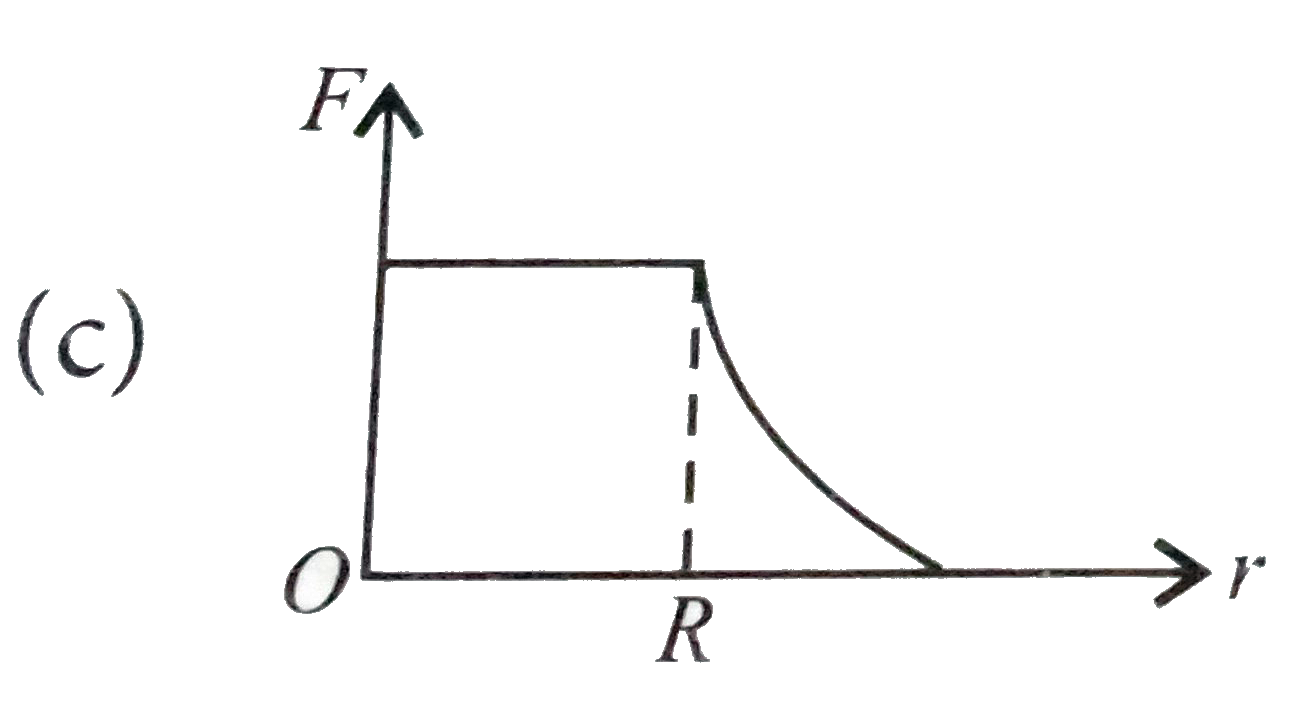 D
D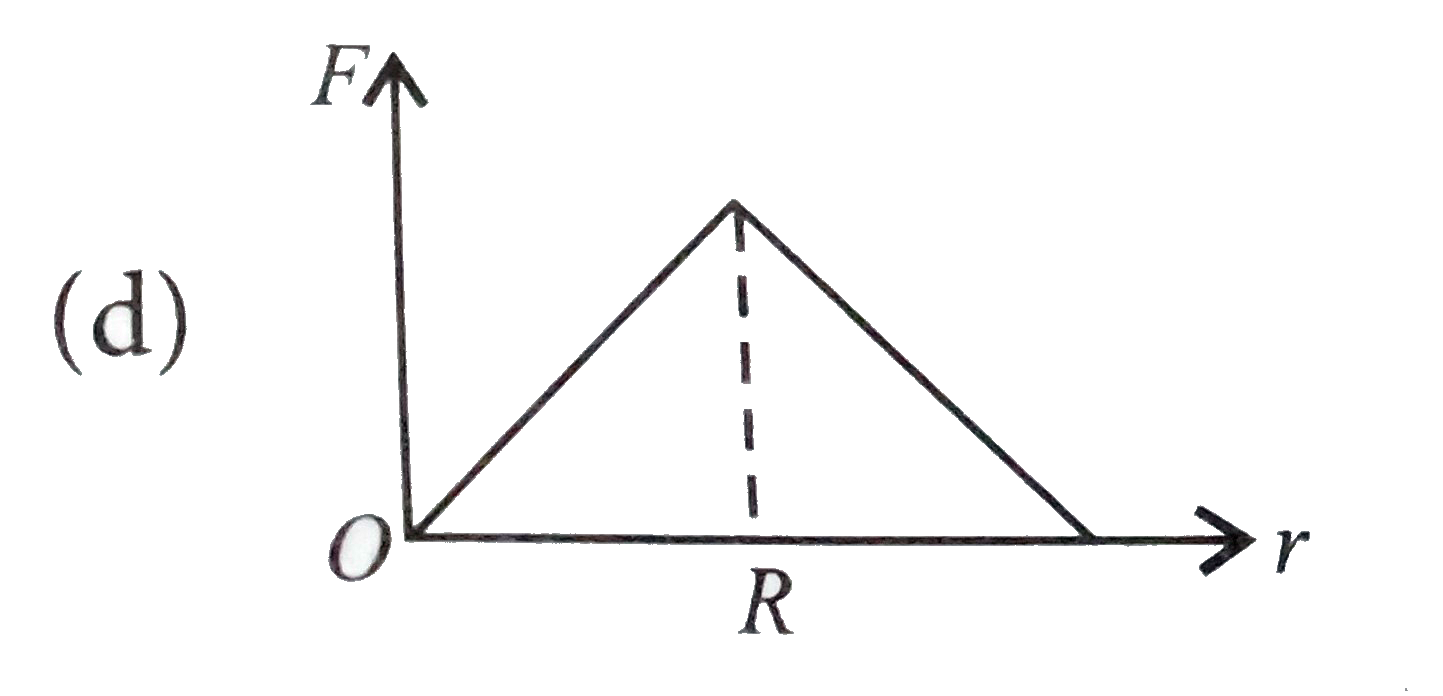
The gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionThe height from the surface of earth at which the gravitational potential energy of a ball of mass m is half of that at the centre of earth is (where R is the radius of earth)
View SolutionThe gravitational potential energy at a body of mass m at a distance r from the centre of the earth is U. What is the weight of the body at this distance ?
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionBy which curve will be variation of gravitational potential of a hollow sphere of radius R with distance be depicted ?
View SolutionThe distance of geostationary satellite from the centre of the earth (radius R) is nearest to
View Solution