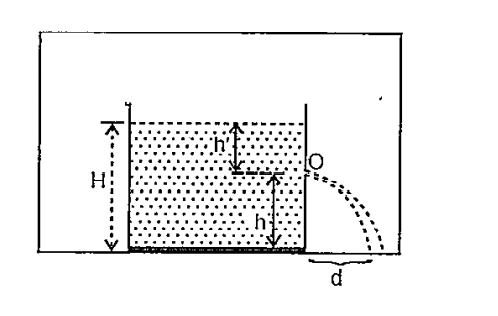
A big container is kept on a horizontal surface of uniform area of cross section. A [Fig. 3.18]. Two non-viscous liquid of densities d and 2d which are not mixed with each other and not compressed, are kept in the container. The height of both liquid column is H2 and the atmospheric pressure on the open surface of the liquid is p0. A small orifice is created at a height h from the bottom of the container. (i) Calculate the initial velocity of efflux of the liquid through the orifice. (ii) Calculate the horizontal distance x at which the first liquid drop emerged from the orifice will reach. (iii) What will be the value of h If the value of the horizontal distance x to be maximum xm ? Also calculate the value of xm neglecting the air resistance.
![A big container is kept on a horizontal surface of uniform area of cross section. A [Fig. 3.18]. Two non-viscous liquid of densities d and 2d which are not mixed with each other and not compressed, are kept in the container. The height of both liquid column is H/2 and the atmospheric pressure on the open surface of the liquid is p0. A small orifice is created at a height h from the bottom of the container. (i) Calculate the initial velocity of efflux of the liquid through the orifice. (ii) Calculate the horizontal distance x at which the first liquid drop emerged from the orifice will reach. (iii) What will be the value of h If the value of the horizontal distance x to be maximum xm ? Also calculate the value of xm neglecting the air resistance.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/CHY_DMB_PHY_XI_P2_U07_C03_SLV_011_Q01.png)
(i) Let, the initial velocity of efflux of the liquid = v.

According to Bernoulli.s theorem,
p0+dg(H2)+2dg(H2−h)=p0+12(2d)v2
or, v2=(H2+2H2−2h)gor,v=√(3H−3h)g2
(ii) The time required to reach the ground of the first liquid drop emerged from the orifice is,
t=√2hg
∴ The horizontal distance traversed by the liquid is,
x=vt=√(3H−4h)g2√2hg
=√h(3H−4h)
(iii) The condition for x to be maximum (xm) :
x=√h(3H−4h)=√−(4h2−3hH)
=
⎷−{(2h)2−2.2h.34H+(34H)2−(34H)2}
=√98H2−(2h−34H)2
∴ x=xmwhen2h−34H=0
Hence, h=38H
∴xm=√98H2=32√2H.
Topper's Solved these Questions
- VISCOSITY AND SURFACE TENSIONBOOK - CHHAYA PUBLICATIONCHAPTER - VISCOSITY AND SURFACE TENSIONEXERCISE - EXERCISE (HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
26 Videos
- VISCOSITY AND SURFACE TENSIONBOOK - CHHAYA PUBLICATIONCHAPTER - VISCOSITY AND SURFACE TENSIONEXERCISE - MCQs
22 Videos
- VECTORBOOK - CHHAYA PUBLICATIONCHAPTER - VECTOREXERCISE - CBSE SCANNER
19 Videos
- WBCHSE QUESTION PAPER -2019BOOK - CHHAYA PUBLICATIONCHAPTER - WBCHSE QUESTION PAPER -2019EXERCISE - SECTION - II ( GROUP -D)
10 Videos
Similar Questions
What is gradient? What is its dimension ?
View SolutionA spherical steel ball released at the top of a long column of glycerin of length L, falls through a distance L/2 with accelerated motion and the remaining distance L/2 with a uniform velocity. If t1andt2 denote the time taken to cover the first and second half and W1andW2 the work done against gravity in the two halves, then
View SolutionA body is projected horizontally from the top of a building of height h. Velocity of projection is u. Find
View SolutionEquations of trajectory of a projectile are x=4 t, y=3t−5t2 , where x and y are in metre and t is in second . Find (i) maximum height attained by the projectille , (ii) horizontal range of the projectile .
View SolutionA container of large uniform cross sectional area A resting on a horizontal surface holds two immiscible non-viscous and incompressible liquids of density d and 3d each of height H/2. The lower density liquid is open to the atmosphere having pressure P_o . A tiny hole of area a (a lt lt A) is punched on the vertical side of the lower container at a height h (0 lt h lt H/2) for which range is maximum.
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d , each of height H//2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L lt (H)/(2)) , cross-sectional area A//5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L//4 denser liquid. Determine (a) density D of the solid and (b) the total pressure at the bottom of the container. (Atmospheric pressure = P_0 ). .
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two-immiscible, non-viscous & incompressible liquids of densities d & 2d, each of height H/2. The lower density liquid is open to the atmoshpere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) corss-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid interface with the length L/4 in the denser liquid. Determine : (i) The density D of the solid & (ii) The total pressure at the bottom of the container.
View SolutionA wide tank of cross-section area A, containing a liquid to a height H, has an orifice at its base of area A/3 . The initial velocity of top surface of liquid is
View SolutionA container with a cross section contains two unmixed liquids of density d and 2d. The height of each of the two liquids in the container frac{H}{2} [Figure 3.57]. The vessel is placed on a horizontal surface. The atmospheric pressure at its opening is rho_ (0). h(h The initial velocity of liquid discharge through the pores is
View SolutionA cylindrical vessel of uniform cross-section contains liquid upto the height' H’ . At a depth H=H2 below the free surface of the liquid there is an orifice. Using Bernoulli's theorem, find the velocity of efflux of liquid.
View SolutionA vessel of large uniform cross-sectional area resting on a horizontal surface holds two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H/2. If a small hole is punched on the vertical side of the container at a heighth h(h<H2) the efflux speed of the liquid al the hole is
View SolutionA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :

View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The density D of the material of the floating cylinder is
View SolutionHeight of liquid is H, depth of orifice from water level is h', height of orifice from bottom is h, radius of orifice is r (very small compare to the cross-section of container). The horizontal distance travelled by the water jet is
View SolutionA container of large uniform cross sectional area A , resting on horizontal surface, holds two immiscible non viscous and incompressible liquids of density d and 2d , each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A tiny hole of area (s(sltltA) is punched on the vertical side of the container at a height h(hltH/2) . Determine The horizontal distance traveled by the liquid, initially, is :
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d , each of height H//2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L lt (H)/(2)) , cross-sectional area A//5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L//4 denser liquid. Determine (a) density D of the solid and (b) the total pressure at the bottom of the container. (Atmospheric pressure = P_0 ). .
View Solution
