A container of large uniform Cross-sectional area holds two immiscible, non-viscous and in compressible liquids of densities p and 4p, each of height H2. The position where small hole has to be punched, so that the heavier liquid comes out with a maximum range R initially is
At a height H4 from the bottom
At a height 58H from the bottom
At a height 516H from the bottom
At a height 718H from the bottom
The correct Answer is:C
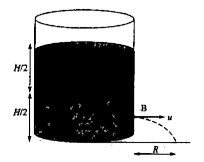
Applying Bernoullis theorem between (A) and (B)
p0+ρgH2+4ρ(H2−h)g=p0+124pu2
ρgH2+2ρgH−4ρgh=124ρu2⇒5ρgH2−4ρgh=124ρu2
u2=14(5gH−8gh)⇒u=12√5gH−8gh
t=√2hg,R=ut=12√5gH−8gh√2hg=12√10Hh−16h2
For R to be maximum, dRdh=0
∴dRdh=1212√10Hh−16h2(10H−32h)=0⇒h=10H32=516H
Similar Questions
A container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
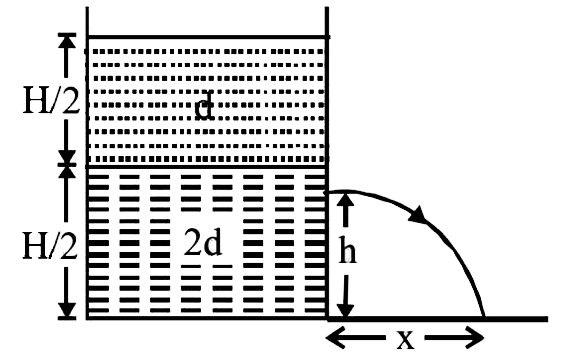
(a) A homogeneous solid cylinder of length L(L<H/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid. Determine:
(i) the density D of the solid and
(ii) the total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). Determine:
(i) the initial speed of efflux of the liquid at the hole,
(ii) the horizontal distance x travelled by the liquid initially, and
(iii) the height hm at which the hole should be punched so that the liquid travels the maximum distance xm initially. Also calculate xm.
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,
The density D of the material of the floating cylinder is
View Solution
Knowledge Check
A container of large uniform cross sectional area A resting on a horizontal surface holds two immiscible non-viscous and incompressible liquids of density d and 3d each of height H/2. The lower density liquid is open to the atmosphere having pressure Po. A tiny hole of area a (a<<A) is punched on the vertical side of the lower container at a height h(0<h<H2) for which range is maximum.
Ah=H/3BRange R=2H/3CRange R=3H/2Dvelocity of efflux r v=√23gHA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder isAv=√g3[3H+4h]Bv=√g3[4H−3h]Cv=√g3[3H−4h]DNone of theseA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial value of x isA√(3H+4h)hB√(3h+4H)hC√(3H−4h)hD√(3H−3h)h
A container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L<H2), cross-sectional area A/5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L/4 denser liquid. Determine
(a) density D of the solid and
(b) the total pressure at the bottom of the container. (Atmospheric pressure =P0).
 .
.
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L<H2), cross-sectional area A/5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L/4 denser liquid. Determine
(a) density D of the solid and
(b) the total pressure at the bottom of the container. (Atmospheric pressure =P0).
 .
.
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial value of x is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The density D of the material of the floation cylinder is
View Solution
