Two circles C1andC2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB,andQY meets circles C1andC2 at XandZ , respectively. Then prove that Y is the midpoint of XZ.
Step by step video & image solution for Two circles C_1a n dC_2 intersect at two distinct points Pa n dQ in a line passing through P meets circles C_1a n dC_2 at Aa n dB , respectively. Let Y be the midpoint of A B ,a n dQ Y meets circles C_1a n dC_2 at Xa n dZ , respectively. Then prove that Y is the midpoint of X Zdot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
In figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ || seg RP.

View SolutionConsider two lines L1andL2 given by a1x+b1y+c1=0anda2x+b2y+c2=0respectivelywherec1andc2≠0, intersecting at point P.A line L3 is drawn through the origin meeting the lines L1andL2 at AandB, respectively, such that PA=PB . Similarly, one more line L4 is drawn through the origin meeting the lines L1andL2 at A1andB2, respectively, such that PA1=PB1. Obtain the combined equation of lines L3andL4.
View SolutionIn the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ ∣∣ seg RP.

View SolutionAs shown in the adjoining figure , two circles centred at A and B are touching at C. Line passing through C intersects the two circles at M and N respectively.
Show that seg AM ∣∣seg BN.
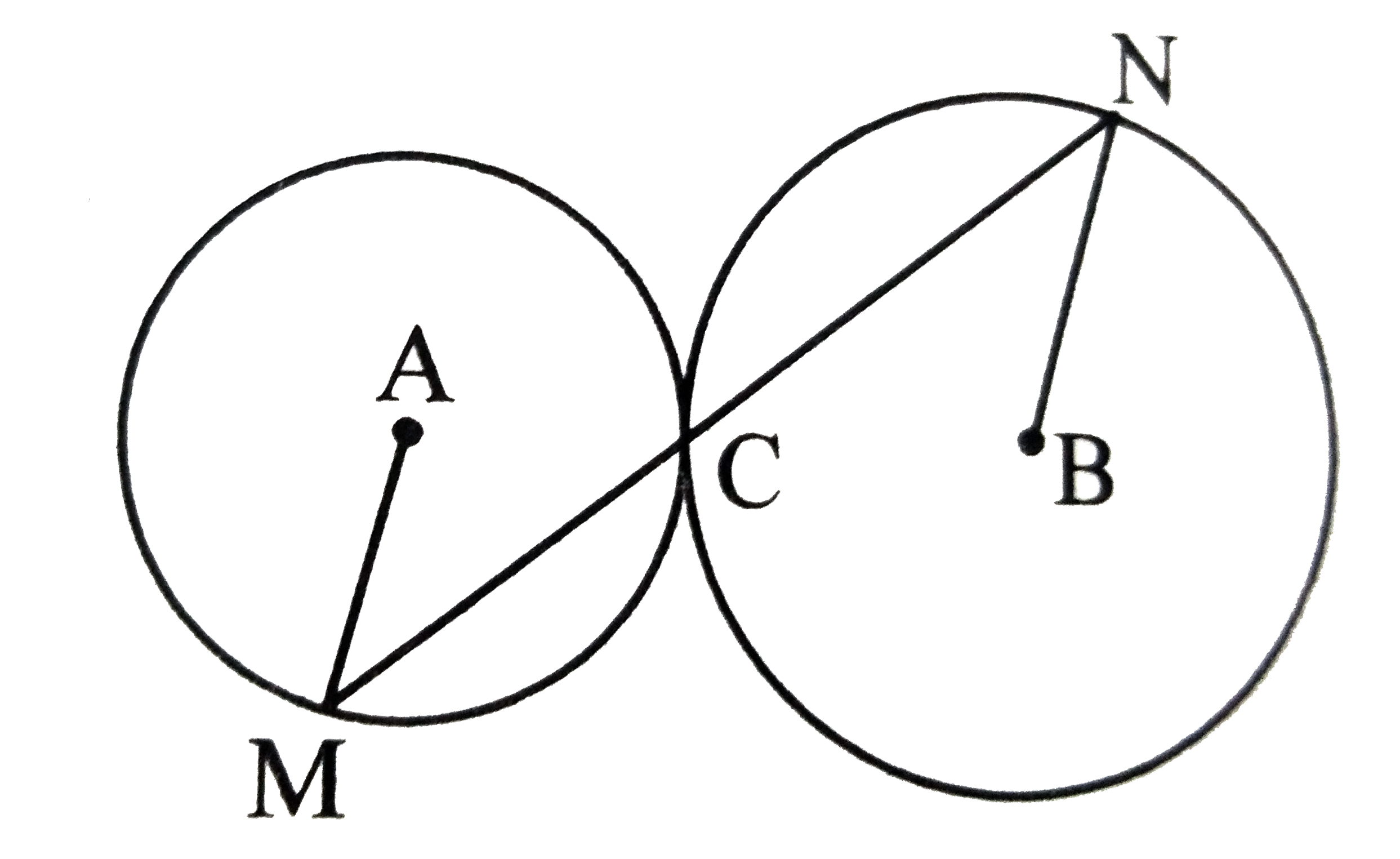
View SolutionThe tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
View SolutionIn figure, ABE is a in which AE=BE . Circle passing through A and B intersects AE and BE at D and C respectively. Prove that DC∣∣AB.
View SolutionTwo circles with centres AandB of radii 3cmand4cm respectively intersect at two points CandD such that ACandBC are tangents to the two circles. Find the length of the common chord CD.
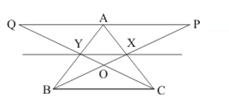
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
View SolutionLet the base AB of a triangle ABC be fixed and the vertex C lies on a fixed circle of radius r. Lines through AandB are drawn to intersect CBandCA, respectively, at EandF such that CE:EB=1:2andCF:FA=1:2 . If the point of intersection P of these lines lies on the median through AB for all positions of AB, then the locus of P is a circle of radius r2 a circle of radius 2r a parabola of latus rectum 4r a rectangular hyperbola
View SolutionLet z1andz2 b be toots of the equation z2+pz+q=0, where he coefficients pandq may be complex numbers. Let AandB represent z1andz2 in the complex plane, respectively. If ∠AOB=θ≠0andOA=OB,whereO is the origin, prove that p2=4qcos2(θ/2).
View Solution
