In figure, BD an CE interesct each other at point P. is triangle PBC - triangle PDE? Why?
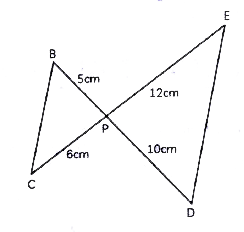
The correct Answer is:Yes
Step by step video, text & image solution for In figure, BD an CE interesct each other at point P. is triangle PBC - triangle PDE? Why? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER (SA-II) TYPE QUESTIONS21videos
TRIANGLES
- BOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS10videos
TRIANGLES
- BOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - VERY SHORT QUESTIONS10videos
TRIANGLES
- BOOK - EDUCART PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS30videos
SURFACE AREAS AND VOLUMES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, BD and CE are the altitudes of triangle ABC such that BD = CE, then

∠DCB=A∠EBCB∠ECBC∠ABDD∠DBC - Question 2 - Select One
In the given figure, BD and CE are the altitudes of triangle ABC such that BD = CE, then

ΔCBD is congruent toAΔCBEBΔBCECΔBECDΔECB
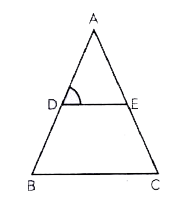
In the given figure, if ∠D=∠C, then it is true that △ADE~△ACB? Why?
 View Solution
View SolutionIn the figure given below altiudes AD and CE of ΔABC intersect each other at the point P. Show that .
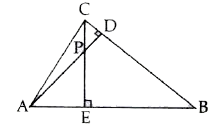
ΔABD~ΔCBEView SolutionIn the figure given below altiudes AD and CE of ΔABC intersect each other at the point P. Show that .
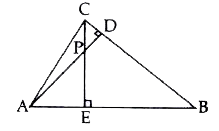
ΔAEP~ΔCDPView SolutionIn the figure , altitudes AD and CE of ΔABC intersect each other at the point P . Show that :
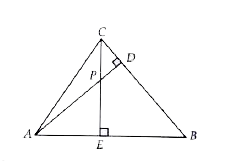
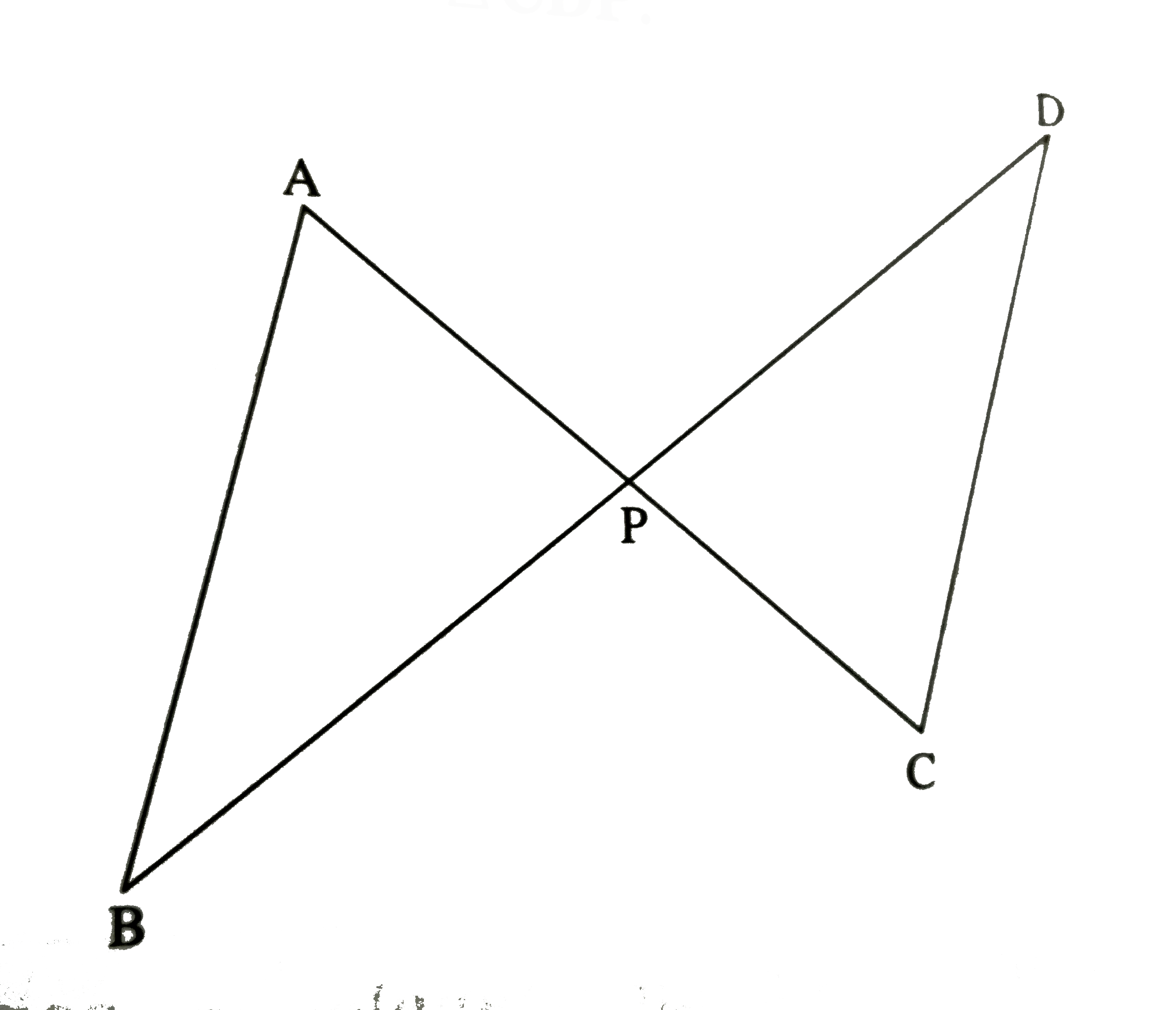
ΔAEP~ΔCDPView SolutionIn the figure, set aC and seg BD intersect each other in point P and APCP=BPDP. Prove that ΔABP~ΔCDP.
 View Solution
View SolutionIn the figure, seg AC and seg BD intersect each other in point P and APCP=BPDP. Prove that ΔABP~ΔCDP.
View Solution


