Derive an expression for electrostatic potential due to an electric dipole.

Text Solution

Verified by Experts

(i) AB be the electric dipole ( -q at A tna +q at B).
2a be the distance between -q and +q.
.r. be the distance between the point .p. and mid point .O. of AB.
$. θ .$ be the angle between OP and OB.

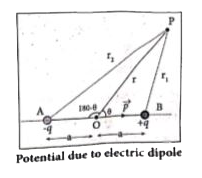
(ii) Let $r_{1}$ be the distance of point P from +q and $r_{2}$ be the distance of point P from -q.
Potential at P due to charge +q $= \frac{1}{4 π ε_{0}} \frac{q}{r_{1}}$
Potential at P due to charge -q $= - \frac{1}{4 π ε_{0}} \frac{q}{r_{2}}$
Total potential at the point p,
$V = \frac{1}{4 π ε_{0}} q (\frac{1}{r_{1}} - \frac{1}{r_{2}}) ....(1)$
(iii) By the cosine law for triangle BOP.
$r_{1}^{2} = r^{2} + a^{2} - 2 r a cos θ$
$r_{1}^{2} = r^{2} (1 + \frac{a^{2}}{r^{2}} - \frac{2 a}{r} cos θ)$
Since a a $< <$ r, term $\frac{a^{2}}{r^{2}}$ is very small and can be neglected. Therefore
$r_{1}^{2} = r^{2} (1 - 2 a \frac{cos θ}{r})$
(or) $r_{1} = r {(1 - \frac{2 a}{r} cos θ)}^{\frac{1}{2}}$
$\frac{1}{r_{1}} = \frac{1}{r} {(1 - \frac{2 a}{r} cos θ)}^{\frac{1}{2}}$
(iv) Using binamial theorem we get.
$\frac{1}{r_{1}} = \frac{1}{r} (1 + \frac{a}{r} cos θ) ...(2)$
Similarly applying the cosne law for triangle AOP,
$r_{2}^{2} = r^{2} - a^{2} - 2 r a cos (180 - θ)$
Since cos ( $180 - θ$ ) = $- cos θ$ we get
$r_{2}^{2} = r^{2} + a^{2} + 2 r a cos θ$
Neglecting $\frac{a^{2}}{r^{2}}$ ( because $r > > a$ )
$a_{2}^{2} = r^{2} (1 + \frac{2 a cos θ}{r})$
$r_{2} = r {(1 + \frac{2 a cos θ}{r})}^{\frac{1}{2}}$
Using Binomial theorem we get
$\frac{1}{r_{2}} = \frac{1}{r} (1 - a \frac{cos θ}{r}) ...(3)$
Substituting equation (3) and (2) in equation (1),
$V = \frac{1}{4 π ε_{0}} q (\frac{1}{r} (1 + a \frac{cos θ}{r}) - \frac{1}{r} (1 - a \frac{cos θ}{r}))$
$V = \frac{q}{4 π ε_{0}} (\frac{1}{r} (1 + a \frac{cos θ}{r}) - \frac{1}{r} (1 - a \frac{cos θ}{r}))$
$V = \frac{1}{4 π ε_{0}} \frac{2 a q}{r^{2}} cos θ$
(v) But the electric dipole moment p = 2qa and we get,
$V = \frac{1}{4 π ε_{0}} (\frac{p cos θ}{r^{2}})$
If p $cos θ = \to p \cdot ˆ r,$ where $ˆ r$ is the unit vector from the point O to point P. then
$V = \frac{1}{4 π ε_{0}} \frac{\to p \cdot ˆ r}{r^{2}} (r > > a) ...(4)$
Spacial cases
Case (i) If the point P lies on the axial line then $θ = 0$ , then
$v = \frac{1}{4 π ε_{0}} \frac{p}{r^{2}} ...(5)$
Case (ii) If the point P lien on the axial line then $θ = 180^{\circ}$ , then
$V = \frac{1}{4 π ε_{0}} \frac{p}{r^{2}} ...(6)$
Case (iii) If the point P lies on the equatorial line, then $θ = 90^{\circ}$ . Hence
V = 0 ...(7)

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile