Derive an expression for electrostatic potential due to a point charge . Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Electric potential due to point charge : Comnsider a positive charge q kept fixed at the origin . Let P be a point at distance r from the charge q . The electric potential at the point P is
$V = \int_{\infty}^{r} (- \to E) . d \to r = - \int_{\infty}^{r} \to E d \to r \dots (1)$

Electric field due to positive point charge q is
$\to E = \frac{1}{4 π ε_{0}} \frac{q}{r^{2}} ˆ r V = \frac{- 1}{4 π ε_{0}} \int_{\infty}^{r} \frac{q}{r^{2}} ˆ r . d \to r$
The infinitesimal displacement vector $d \to r = d r \to r$ and using $ˆ r . ˆ r = 1$ , we have
$V = - \frac{1}{4 π ε_{0}} \int_{\infty}^{r} \frac{q}{r^{2}} ˆ r . d r ˆ r = - \frac{1}{4 π ε_{0}} \int_{\infty}^{r} \frac{q}{r^{2}} d r$
After the integration $V = - \frac{1}{4 π ε_{0}} q {- \frac{1}{r}}_{\infty}^{r} = \frac{1}{4 π ε_{0}} \frac{q}{r}$
Hence the electric potential due to a point charge q at a distance r is
$V = \frac{1}{4 π ε_{0}} \frac{q}{r}$
Important points ( If asked in exam )
(i) If the source charge q is positive $V > 0 .$ If q is negative then V is negative and equal to
$V = \frac{1}{4 π ε_{0}} \frac{q}{r}$
(ii) The description of objects using the concept of potential or potential energy is simpler than that using the concept of field.
(iii) From expression (2) it is clear that the potential due to positive charge decreases as the distance increases but for a negative charge the potential increases as the distance is increased . At infinity ( $r = \infty$ ) electrostatic potential is zero( V=0).
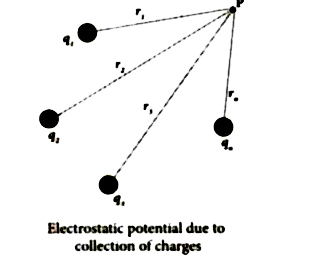
(iv) The electric potential at a point P due to a collection of charges $q_{1}, q_{2}, q_{3} \dots q_{n}$ is equal to sum of the electric potentials due to individual charges .
$V_{tot} = \frac{k q_{1}}{r_{1}} + \frac{k q_{2}}{r_{2}} + \frac{k q_{3}}{r_{3}} + \dots + \frac{k q_{n}}{r_{n}} = \frac{1}{4 π ε_{0}} n \sum i = 0 \frac{q_{i}}{r_{i}}$
where $r_{1}, r_{2}, r_{3}, \dots, r_{n}$ are the distances of $q_{1}, q_{2}, q_{3} \dots, q_{n}$ respectively from P

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

FULL MARKS-ELECTROSTATICS -Textual Evaluation Solved ( III. Long Answer Questions: )

Home
Ask Doubt
Profile