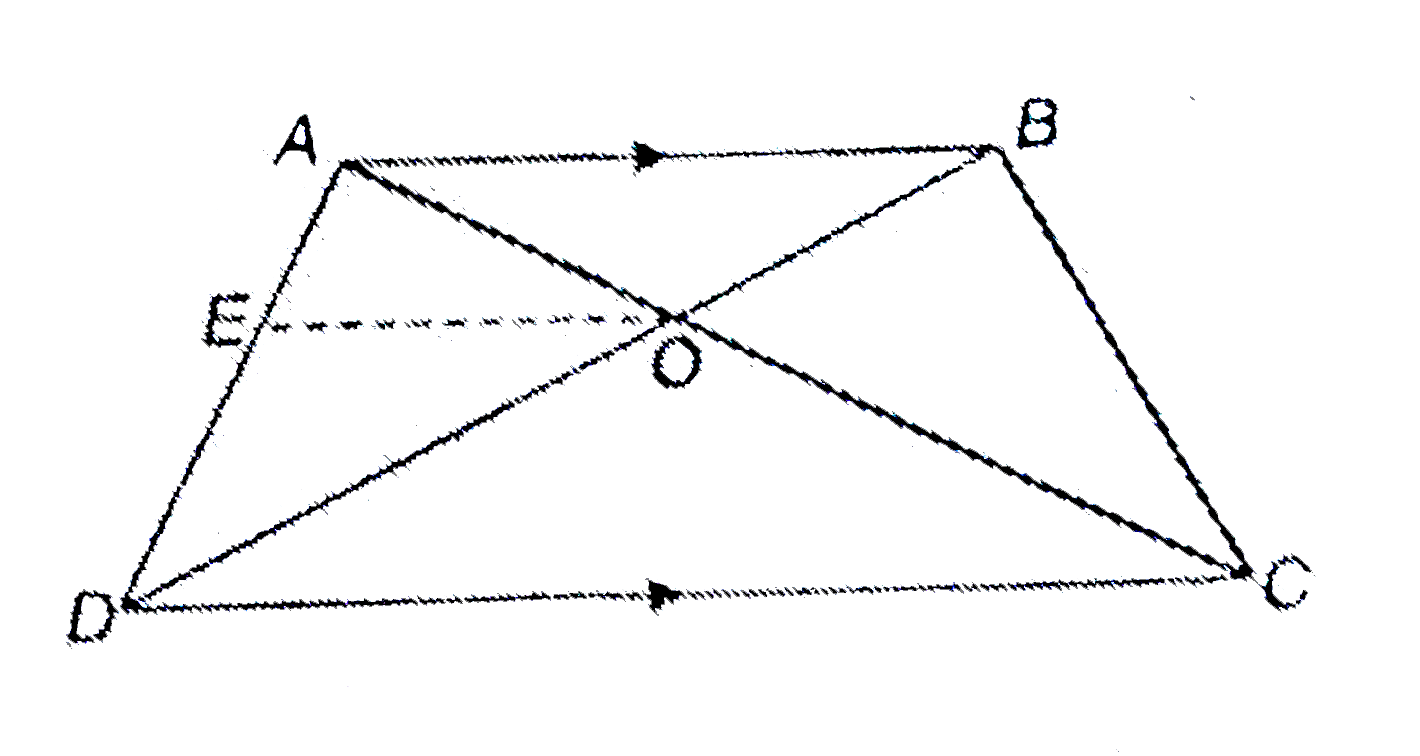
In a quadrilateral ABCD, it is given that $A B ∣ ∣ C D$ and the diagonals $A C and B D$ are perpendicular to each other. Show that $A D . B C \geq A B . C D$ .

Video Solution

Text Solution

Verified by Experts

Let AC and BD intersect at O (origin)
According to the question $\to a . \to b = 0$
Also AB||CD
$(μ \to a - λ \to b) ∣ ∣ (\to a - \to b)$
$\Rightarrow μ = λ$
$L e t A D . B C \geq A B . C D$
$\Rightarrow ∣ ∣ λ \to b - \to a ∣ ∣ ∣ ∣ μ \to a - \to b ∣ ∣ | \geq | (\to b - \to a) ∣ ∣ ∣ (λ \to b - μ \to a) ∣ ∣$
$or (λ^{2} b^{2} + a^{2}) (μ^{2} a^{2} + b^{2}) \geq (b^{2} + a^{2}) (λ^{2} b^{2} + μ^{2} a^{2})$
$or λ^{2} μ^{2} a^{2} b^{2} + a^{2} b^{2} \geq λ^{2} a^{2} b^{2} + μ^{2} b^{2} a^{2}$
$or (λ^{92}) - 1) (μ^{2} - 1) \geq 0$
$or {(λ^{2} - 1)}^{2} \geq 0$ which is true.
Hence, AD. BC $\geq$ AB. CD

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

CENGAGE-DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS -Exercise

Home
Ask Doubt
Profile