In Fig. 10.37, ∠PQR = 100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR.
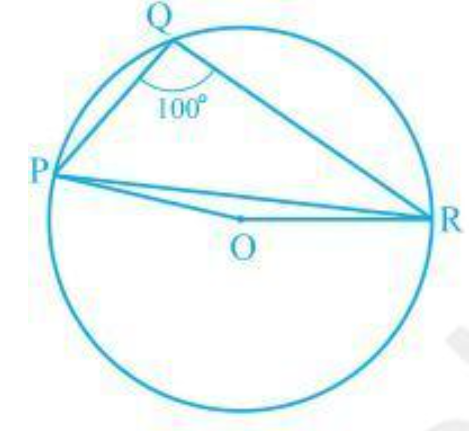
Since all points P,Q,R,S lie on the circle, PQRS becomes a cyclic quadrilateral.
We know that the sum of either pair of opposite angles of a cyclic quadrilateral is 180∘
Therefore,∠PQR+∠PSR=180∘
100∘+∠PSR=180∘
∠PSR=180∘−100∘=80∘
We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle
Therefore,∠POR=2∠PSR
= 2×80∘
= 160∘
Consider the △OPR. It is an isosceles triangle as OP=OR = Radius of the circle.
Thus, ∠OPR=∠ORP
Sum of all angles in a triangle is 180∘
Therefore,
∠OPR+∠POR+∠ORP=180∘
∠OPR+160∘+∠OPR=180∘
2∠OPR=180∘−160∘
∠OPR=10∘
Topper's Solved these Questions
- CIRCLESBook:NCERTChapter:CIRCLESExercise:EXERCISE 10.2
Explore 2 Videos
- CIRCLESBook:NCERTChapter:CIRCLESExercise:Exercise 10.4
Explore 6 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:NCERTChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:EXERCISE 9.1
Explore 1 Video
- CONSTRUCTIONSBook:NCERTChapter:CONSTRUCTIONSExercise:EXERCISE 11.2
Explore 5 Videos
Similar Questions
Knowledge Check
Let P and Q be two points on a circle with centre O. If two tan gents of the circle through P and O meet at A with ∠PAQ=48∘, then ∠APQ is
A96∘B48∘C66∘D60∘
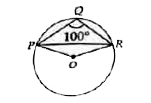
In the given figure, ∠PQR=100∘, where P, 9 and R are points on a circle with centre O. Find ∠OPR.

View SolutionIn the given figure ∠PQR=100∘, where P,Q,R are points on a chords with centre O. Find the measure of ∠OPR.
View SolutionIn Fig. 10.95, PQ and PR are tangents drawn from P to a circle with centre O . If ∠OPQ=35o , then (FIGURE) a=30o, b=60o (b) a=35o, b=55o (c) a=40o, b=50o (d) a=45o, b=45o
View SolutionIn Fig. 10.88, APB is a tangent to a circle with centre O at point P . If ∠QPB=50o , then the measure of ∠POQ is (FIGURE) 100o (b) 120o (c) 140o (d) 150o
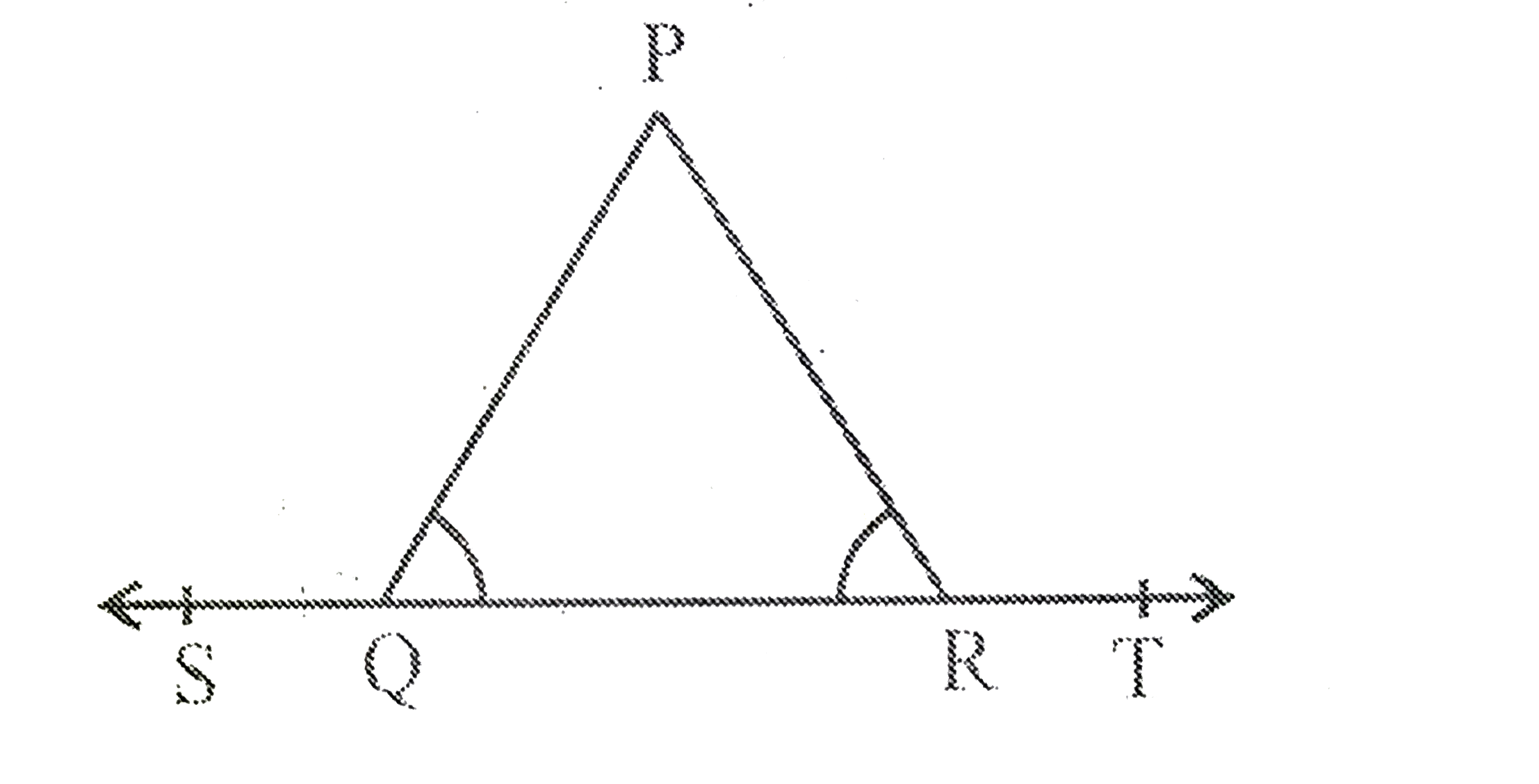
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
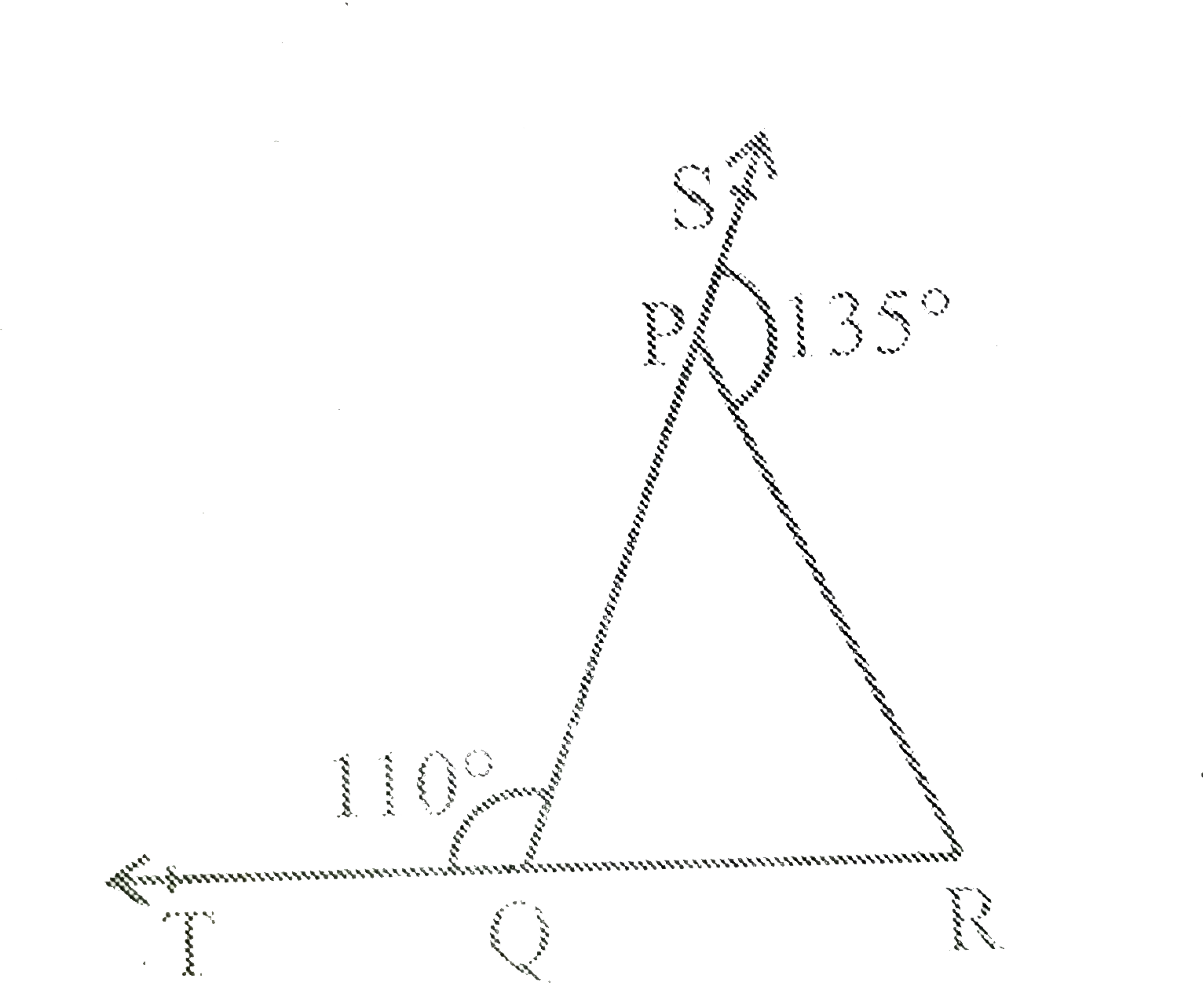
View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
View SolutionThe sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P, Q, and R respectively.
View Solution