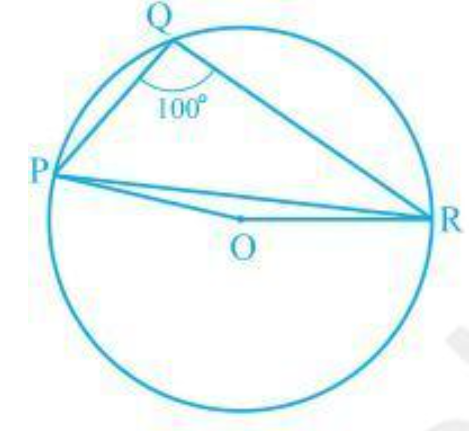
In Figure, ∠PQR=1000, where P, Q and R are points on a circle with centre. O. Find ∠OPR
To solve the problem, we need to find the angle ∠OPR given that ∠PQR=100∘ and P,Q,R are points on a circle with center O.
1. Identify the given information:
We know that ∠PQR=100∘.
2. Relate the angles:
According to the properties of circles, the angle subtended at the center of the circle is twice the angle subtended at any point on the circumference. Therefore, we can express ∠POR (the angle at the center) as:
∠POR=2×∠PQR=2×100∘=200∘
3. Determine the remaining angle:
Since the total angle around point O is 360∘, we can find the acute angle ∠POR by subtracting 200∘ from 360∘:
∠POR=360∘−200∘=160∘
4. Analyze triangle OPR:
In triangle OPR, since OP and OR are both radii of the circle, we have:
OP=OR
This means triangle OPR is isosceles, with OP=OR.
5. Set up the equation for angles in triangle OPR:
Let ∠OPR=∠ORP=x. The sum of angles in triangle OPR is 180∘:
∠OPR+∠ORP+∠POR=180∘
Substituting the known values:
x+x+160∘=180∘
Simplifying gives:
2x+160∘=180∘
6. Solve for x:
Subtract 160∘ from both sides:
2x=180∘−160∘=20∘
Dividing by 2 gives:
x=10∘
7. Conclusion:
Therefore, the angle ∠OPR is:
∠OPR=10∘
Final Answer:
∠OPR=10∘
We know that ∠PQR=100∘.
According to the properties of circles, the angle subtended at the center of the circle is twice the angle subtended at any point on the circumference. Therefore, we can express ∠POR (the angle at the center) as:
∠POR=2×∠PQR=2×100∘=200∘
Since the total angle around point O is 360∘, we can find the acute angle ∠POR by subtracting 200∘ from 360∘:
∠POR=360∘−200∘=160∘
In triangle OPR, since OP and OR are both radii of the circle, we have:
OP=OR
This means triangle OPR is isosceles, with OP=OR.
Let ∠OPR=∠ORP=x. The sum of angles in triangle OPR is 180∘:
∠OPR+∠ORP+∠POR=180∘
Substituting the known values:
x+x+160∘=180∘
Simplifying gives:
2x+160∘=180∘
Subtract 160∘ from both sides:
2x=180∘−160∘=20∘
Dividing by 2 gives:
x=10∘
Therefore, the angle ∠OPR is:
∠OPR=10∘
∠OPR=10∘
Topper's Solved these Questions
Similar Questions
In Figure, ∠PQR=1000, where P, Q and R are points on a circle with centre. O. Find ∠OPR
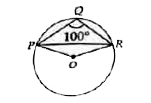
View SolutionIn Fig. 10.37, ∠PQR = 100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR.
View SolutionIn the given figure, ∠PQR=100∘, where P, 9 and R are points on a circle with centre O. Find ∠OPR.

View SolutionIn the given figure ∠PQR=100∘, where P,Q,R are points on a chords with centre O. Find the measure of ∠OPR.
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
View SolutionIn Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
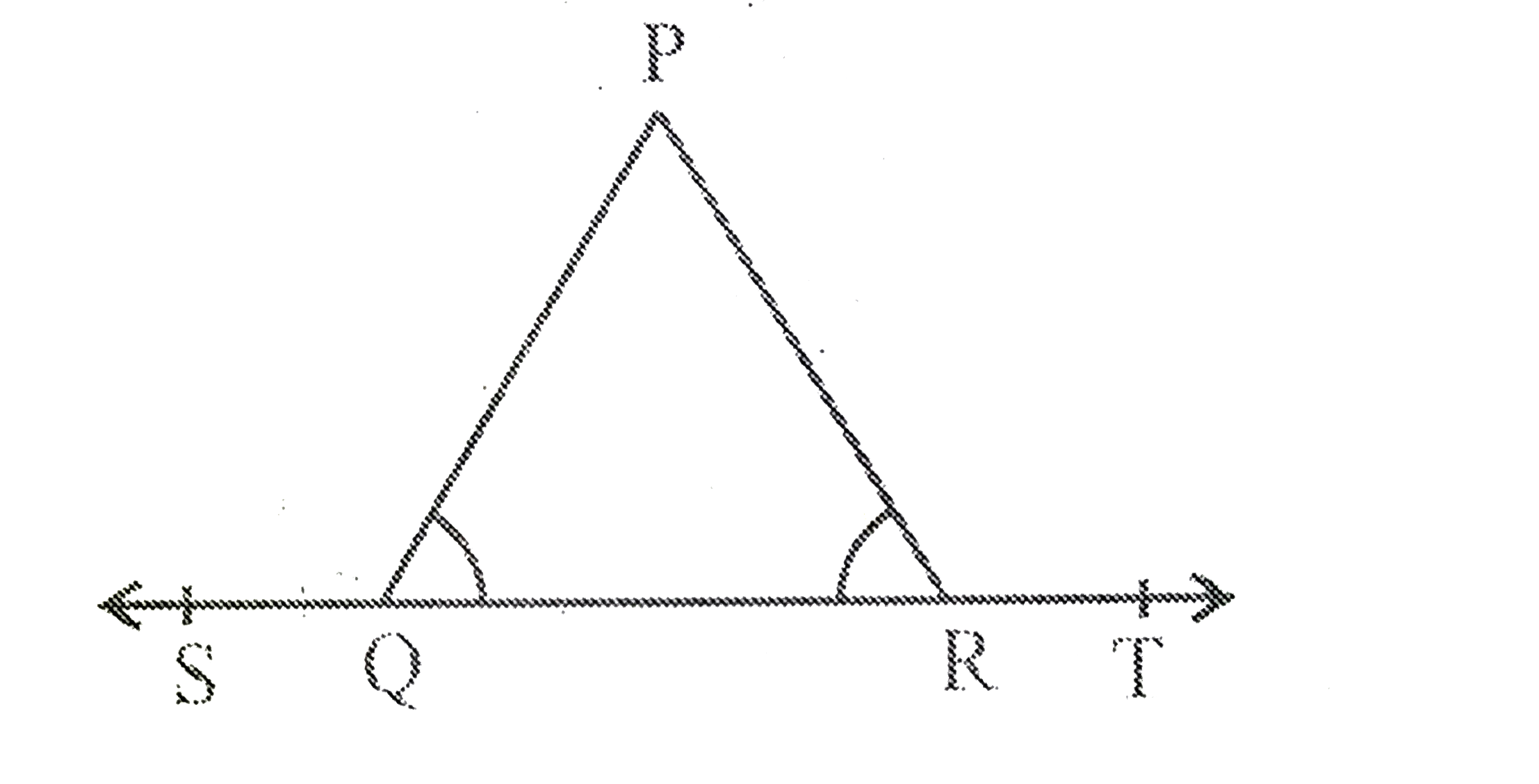
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
View Solution
