$O A B C$ is regular tetrahedron in which $D$ is the circumcentre of $O A B$ and E is the midpoint of edge $A C .$ Prove that $D E$ is equal to half the edge of tetrahedron.

Video Solution

Answer

Step by step video & image solution for O A B C is regular tetrahedron in which D is the circumcentre of O A B and E is the midpoint of edge A Cdot Prove that D E is equal to half the edge of tetrahedron. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Similar Questions

$O A B C$ is regular tetrahedron in which $D$ is the circumcentre of $O A B$ and E is the midpoint of edge $A C .$ Prove that $D E$ is equal to half the edge of tetrahedron.
View Solution
$A B C$ is a triangle in which $D$ is the mid-point of $B C$ and $E$ is the mid-point of $A D .$ Prove that area of $△ B E D = \frac{1}{4} a r e a o f △ A B C .$ GIVEN : A $A B C, D$ is the mid-point of $B C$ and $E$ is the mid-point of the median $A D .$ TO PROVE : $a r (△ B E D) = \frac{1}{4} a r (△ A B C) .$
View Solution
$A B C$ is a triangle. $D$ is a point on $A B$ such that $A D = \frac{1}{4} A B$ and $E$ is a point on $A C$ such that $A E = \frac{1}{4} A C .$ Prove that $D E = \frac{1}{4} B C .$
View Solution
$A B C$ is a triangle. $D$ is a point on $A B$ such that $D = \frac{1}{4} A B a n d E$ is a point on $A C$ such that $A E = \frac{1}{4} A C .$ Prove that $D E = \frac{1}{4} B C$
View Solution
In Figure, $A D$ is the median and $D E ∣ ∣ A B$ . Prove that $B E$ is the median.

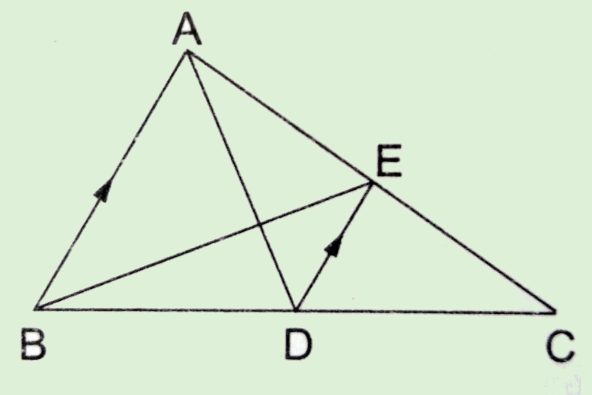
View Solution
$D$ is the mid-point of side $B C$ of $A B C$ and $E$ is the mid-point of $B D .$ If $O$ is the mid-point of $A E$ , prove that $a r (B O E) = \frac{1}{8} a r (A B C)$
View Solution
IF OABC is a tetrahedron where O is the origin and A,B and C have respective positions vectors as $¯ a, ¯ b and ¯ c$ then prove that the circumcentre of the tetrahedron is $\frac{{(¯ a)}^{2} (¯ b \times ¯ c) + {(¯ b)}^{2} (¯ c \times ¯ a) + {(¯ c)}^{2} (¯ a \times ¯ b)}{2 [¯ a ¯ b ¯ c]}$
View Solution
In Figure, it is given that $A E = A D$ and $B D = C E .$ Prove that $A E B ≅ A D C$

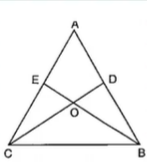
View Solution
OABC is a tetrahedron D and E are the mid points of the edges $- - \to O A$ and $- - \to B C$ . Then the vector $- - \to D E$ in terms of $- - \to O A, - - \to O B and - - \to O C$
View Solution
Regular tetrahedron a tetrahedron whose all the edges are of equal length is called a regular tetrahedron.
View Solution

OABC is regular tetrahedron in which D is the circumcentre of OAB and E is the midpoint of edge AC. Prove that DE is equal to half the edge of tetrahedron.

Similar Questions

Recommended Questions

$O A B C$ is regular tetrahedron in which $D$ is the circumcentre of $O A B$ and E is the midpoint of edge $A C .$ Prove that $D E$ is equal to half the edge of tetrahedron.