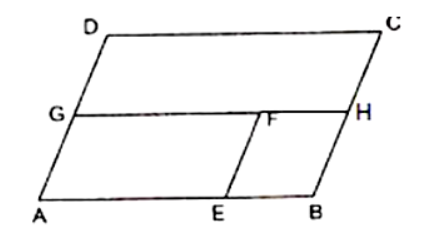
In fig. AB,DEandGF are parallel to each other and AD,BGandEF are parallel to each other. If CD:CE=CG:CB=2:1, then the value of area (AEG): area (ABD) is equal to 7/2 b. 3 c. 4 d. 9/2
Step by step video & image solution for In fig. A B ,D Ea n dG F are parallel to each other and A D ,B Ga n dE F are parallel to each other. If C D : C E=C G : C B=2:1, then the value of area ( A E G): area ( A B D) is equal to 7//2 b. 3 c. 4 d. 9//2 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If a:b=c:d=e:f=1:2, then ( 3a + 5c +7e): (3b + 5d + 7 J) is equal to
A8:7B2:1C1:4D1:2If A:B=1:2,B:C=3:4,C:D=6:9 and D:E=12:16 then A:B:C:D:E is equal to
A1:3:6:12:16B2:4:6:9:16C3:4:8:12:16D3:6:8:12:16If a;b=c:d=e:f=1:2, then (3a+5c+7e):(3b=5d+7f) 1:2 b. 1:4 c. 2:1 d. 8:7
A8:7B2:1C1:4D1:2
In Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
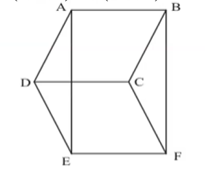
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14AC
View SolutionIn Figure, ABCD is a rectangle with sides AB=10cmandAD=5cm Find the area of EFG

View SolutionThe AD,BEandCF are the medians of a cABC, then (AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View SolutionThe medians AD and BE of a triangle with vertices A(0,b), B(0,0) and C(a,0) are perpendicular to each other, if a=b2 b. b=a2 c. ab=1 d. a=±√2b
View Solution