In fig. 2.33 AB, DE and GF are parallel to each other and AD, BG and EF ar parallel to each other . If CD: CE = CG:CB = 2:1 then the value of area (△AEG):area(△ABD) is equal to

7/2
3
4
9/2
The correct Answer is:b
Let A be the origin, −−→AB=→a,−−→AD=→b
so, −−→AE,→b+32→a,−−→AG=→a+3→b
12∣∣(→a+3→b)×(→b+32→a)∣∣12∣∣→a×→b∣∣
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Single Question)
28 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Multiple Question)
11 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.3
18 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
1316 Videos
- LIMITS AND DERIVATIVESBOOK - CENGAGECHAPTER - LIMITS AND DERIVATIVESEXERCISE - Solved Examples And Exercises
320 Videos
Similar Questions
In AB, DE and GF are parallel to each other and AD, BG and EF ar parallel to each other . If CD: CE = CG:CB = 2:1 then the value of area (△AEG):area(△ABD) is equal to (a) 7/2 (b)3 (c)4 (d)9/2
View SolutionIn fig. AB,DEandGF are parallel to each other and AD,BGandEF are parallel to each other. If CD:CE=CG:CB=2:1, then the value of area (AEG): area (ABD) is equal to 7/2 b. 3 c. 4 d. 9/2
View Solution
Knowledge Check
D and E are points on sides AB and AC of ΔABC. DE is parallel to BC. If AD : DB = 2 : 3, what is the ratio of area ΔADE and area of quadrilateral BDEC ?
A4:21B4:25C4:29D4:9
In quadrilateral ABCD, AB=DC and AD=BC. Prove that the sides AB and DC are parallel to each other.
View SolutionIn quadrilateral ABCD, AB=DC and AD=BC. Prove that the sides AB and DC are parallel to each other.
View SolutionIn the figure, P is the centre of the circle. Two chords AB and CD are parallel to each other. Prove ∠CPA=∠DPB.
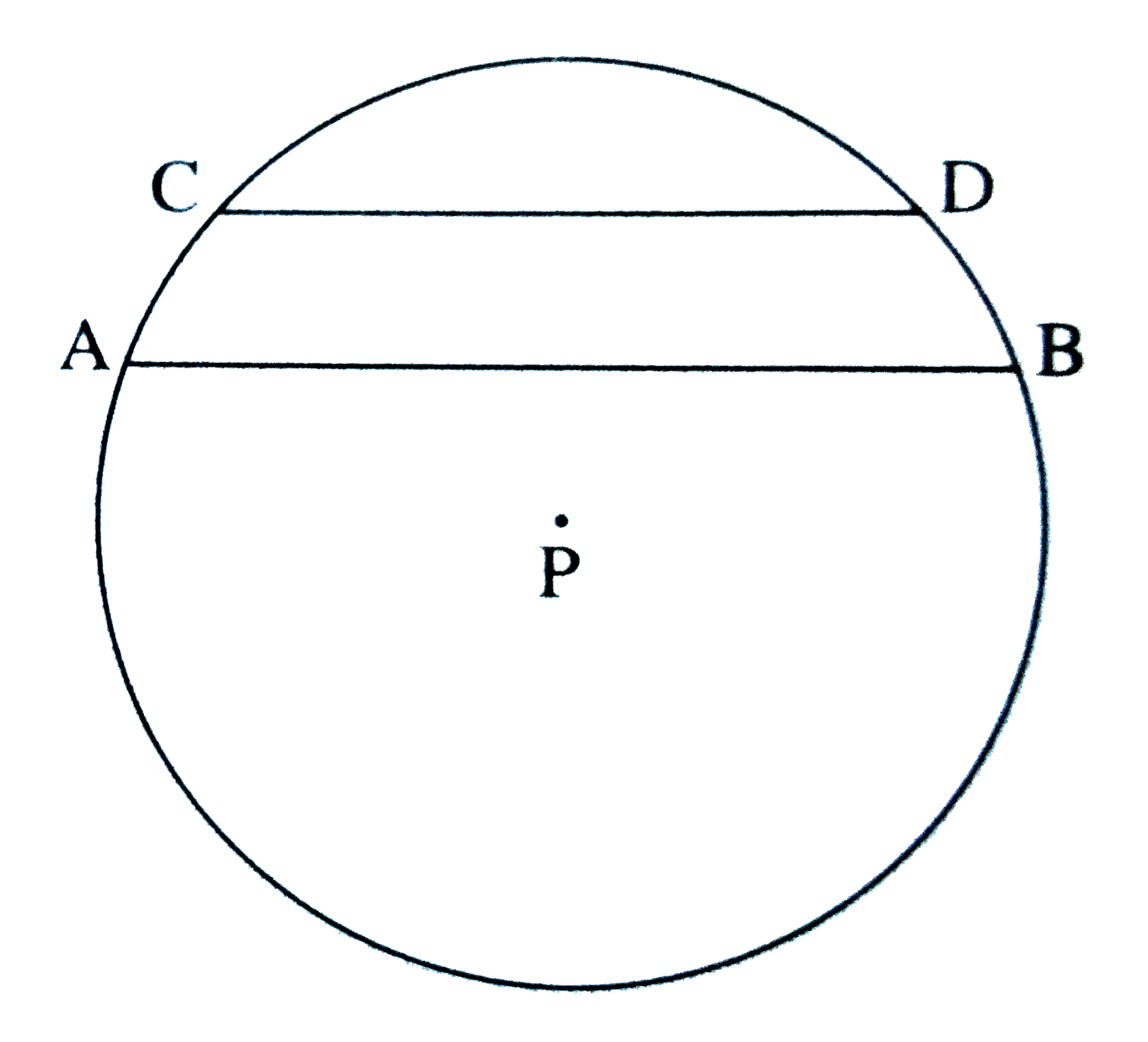
View SolutionIn the given figure, lines AB,CD and EF are parallel to each other. Find th values of ∠x,∠y,∠z and ∠p
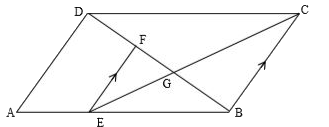
View SolutionIn the figure given below, ABCD is a parallelogram. E is a point on AB. CE intersects the diagonal BD at G and EF is parallel to BC.
If AE : EB = 1 : 2 find
area of triangle BEF : area of triangle ABD
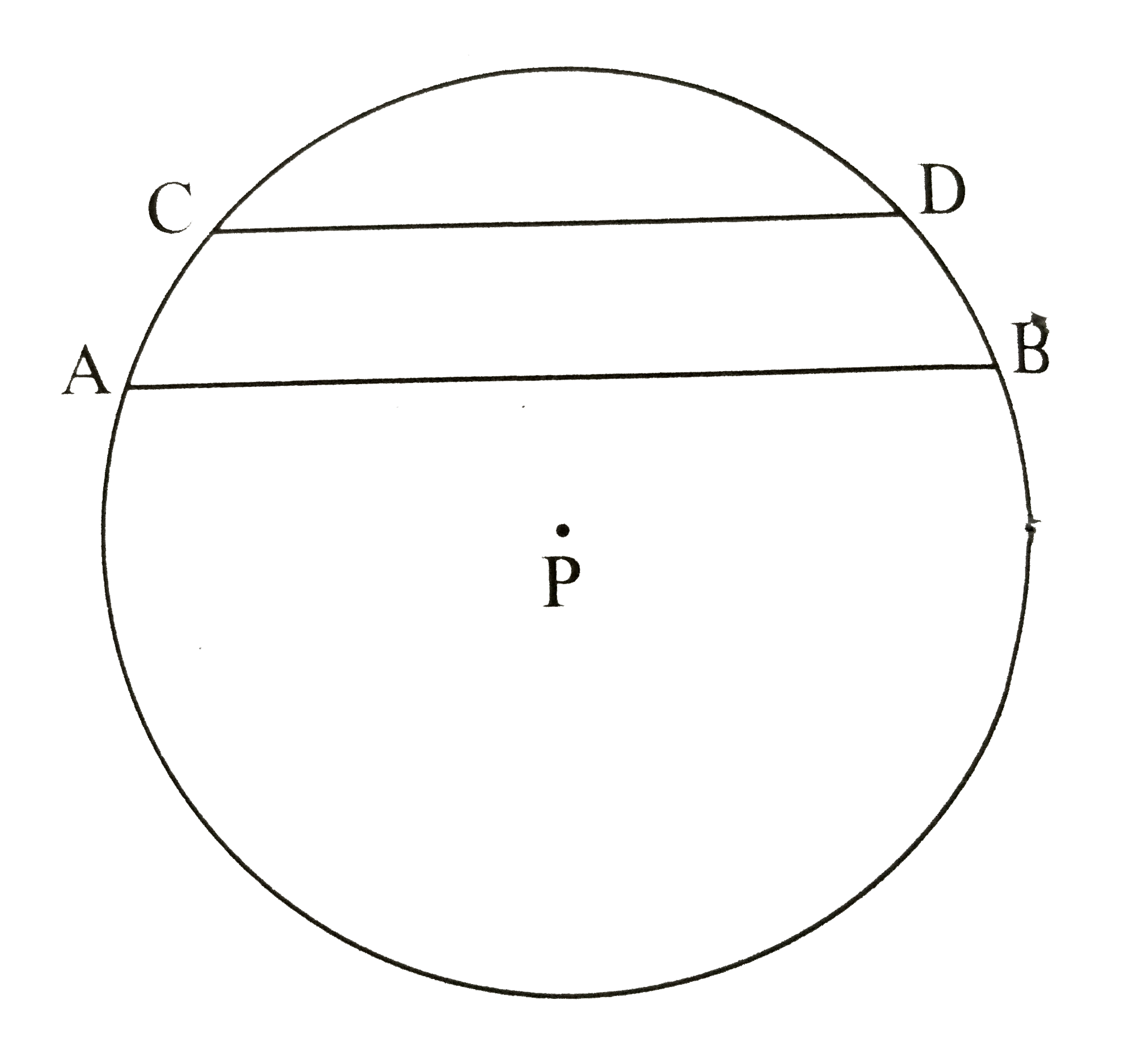
View SolutionIn the figure, two chords AB and CD are parallel to each other. P is the centre of the circle.
Show that ∠CPA≅∠DPB .
View SolutionIn trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that : AB + DC = 2EF.
View Solution
