Two trolleys of masses m and 3m are connected by a spring. They are compressed and released, they move off in opposite direction and come to rest after covering distances s1ands2 respectively. If the frictional force between trolley and surface is same in both the cases then the ratio of distances s1:s2 is
1:9
1:3
3:1
9:1
The correct Answer is:D
m1v2=m2v2,s1s2=(v1v2)2
Topper's Solved these Questions
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (C.W)(EQUILIBRIUM OF A PARTICLE)
3 Videos
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (C.W)(MOTION ON A HORIZONTAL ROUGH SURFACE)
10 Videos
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (C.W)(OBJECTS SUSPENDED BY STRINGS AND APPARENT WEIGHT)
21 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
Similar Questions
Two trolleys of masses m and 3 m are connected by a spring. The spring is compressed and released the trolleys move off in opposite directions and come to rest after travelling distances s1, and s2, respectively. Assuming coefficient of friction is same for both the ratio of sto s1 to s2 is
View SolutionTwo light trollwys of masses m1 and m2(=3m1) are connected by a spring. The spring is compressed and bound by a cord. The cord is burnt through, the spring expands and the trolleys move off in opposite direction. Assume that the coefficient of friction is the same for both trollwys.
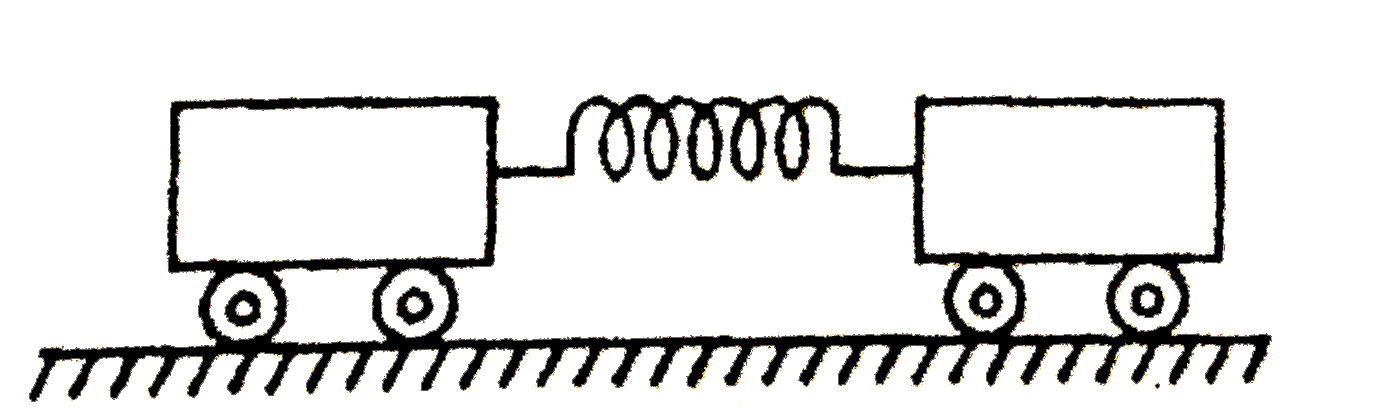
View Solution
Knowledge Check
Two trolleys of mass m and 3m are attached by a spring. The spring was compressed and then released , they move off in opposite direction and comes to rest after covering distances s1 and s2 respectively. Assuming the coefficient of friction to be uniform , the ratio of distances s1:s2 is
A1:9B1:3C3:1D9:1Two light trollwys of masses m1 and m2(=3m1) are connected by a spring. The spring is compressed and bound by a cord. The cord is burnt through, the spring expands and the trolleys move off in opposite direction. Assume that the coefficient of friction is the same for both trollwys.
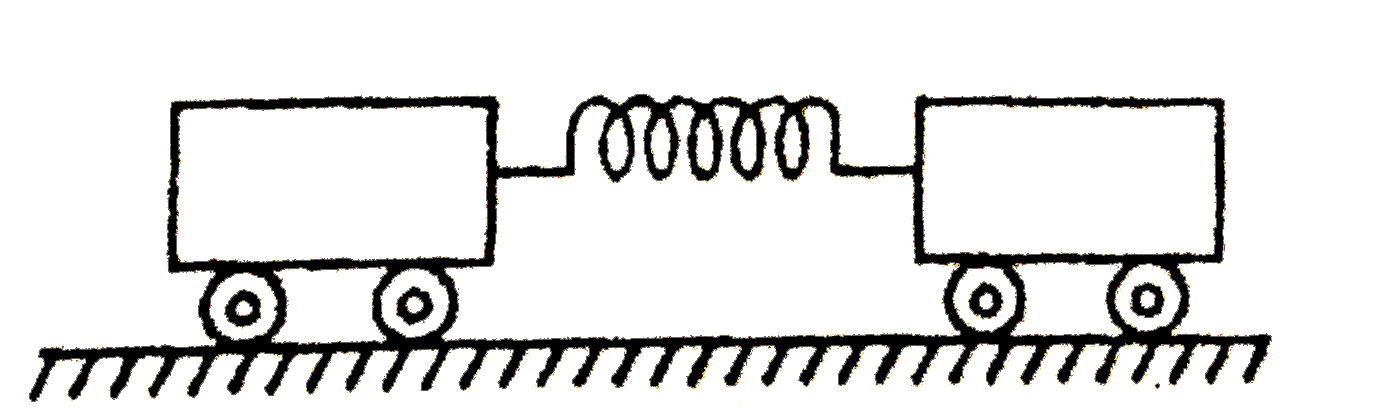 AThe relationship between the velocties v1 and v2 of the trolleys is v1/v2=3BThe relationship between the periods t1 and t2 during which the trolleys move t1/t2=3CThe relationship between the distance s1 and s2 travelled by the trolleys is s1/s2=3DThe relationship between the force of friction f1 and f2 acting on the two trolleys is f1/f2=13
AThe relationship between the velocties v1 and v2 of the trolleys is v1/v2=3BThe relationship between the periods t1 and t2 during which the trolleys move t1/t2=3CThe relationship between the distance s1 and s2 travelled by the trolleys is s1/s2=3DThe relationship between the force of friction f1 and f2 acting on the two trolleys is f1/f2=13A body of mass m is travelling with a velocity vu. When a constant retarding force F is applied, it comes to rest after travelling a distance s1. If the initial velocity is 2u with the same force F, the distance travelled before it comes to rest is s2. then,
As2=4s1B2s2=2s1Cs2=s12Ds2=s1
Two masses m1andm2 re connected by a spring of spring constant k and are placed on as frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
View SolutionTwo masses m1andm2 re connected by a spring of spring constnt k and are placed on as frictionless horizontal surface. Initially the spring is tretched through a distance x0 when the system is released from rest. Find the distance moved by the tow masses before they again come to rest.
View SolutionA body moving on the ground with a velocity of 15m/s comes to rest after covering a distance of 25m If acceleration due to gravity is 10m/s2 Calculate the coefficient of friction between the ground and the body .
View SolutionTwo blocks of masses m and 3m on a horizontal surface are in contact with the ends of a horizontal massless spring. The coefficient of friction between m and surface and between 3m and surface is μ and μ/3 respectively. The two blocks are moved towards each other to compress the spring and then released. The two blocks move off in opposite directions covering distances S1 and S2 before comming to rest. S1:S2 is
View SolutionA block slides with a velocity of 10 m/s on a rough horizontal surface. It comes to rest after covering a distance of 50 metre. If g is 10m/s2, then the coefficient of dynamic friction between the block and the surface is
View Solution
