A boy is hanging from a horizontal branch of a tree. The tension in the arms will be maximum when the angle between the arms is
A
0∘
B
60∘
C
90∘
D
120∘
Video Solution
Text Solution
The correct Answer is:D
2Tcosθ↑=Mg
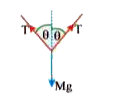
T=(Mg2cosθ)
Tmax⇒cos (min)
|
Topper's Solved these Questions
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - IV
35 Videos
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (H.W)(CIRCULAR MOTION)
3 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
Similar Questions
Knowledge Check
A boy of mass 40 kg is hanging from the horizontal branch of a tree. The tension in his arms is minimum when the angle between the arms is:-
A0∘B90∘C120∘D180∘The roots hanging from the branches of banyan tree are
APrimary rootsBFibrous rootCProp rootsDPneumatophoresRoots that hold horizontal branches of Banyan tree in the air are
AThumb rootsBProp rootsCStlit rootsDAll the above.
Show that the horizontal range is maximum when the angle of projection is 45∘
View SolutionRoots arises from the horizontal arial branches of tree Banyan is called
View SolutionRoot which grow from branches of Banyan tree are
View SolutionThe hanging root from the banyan tree is called
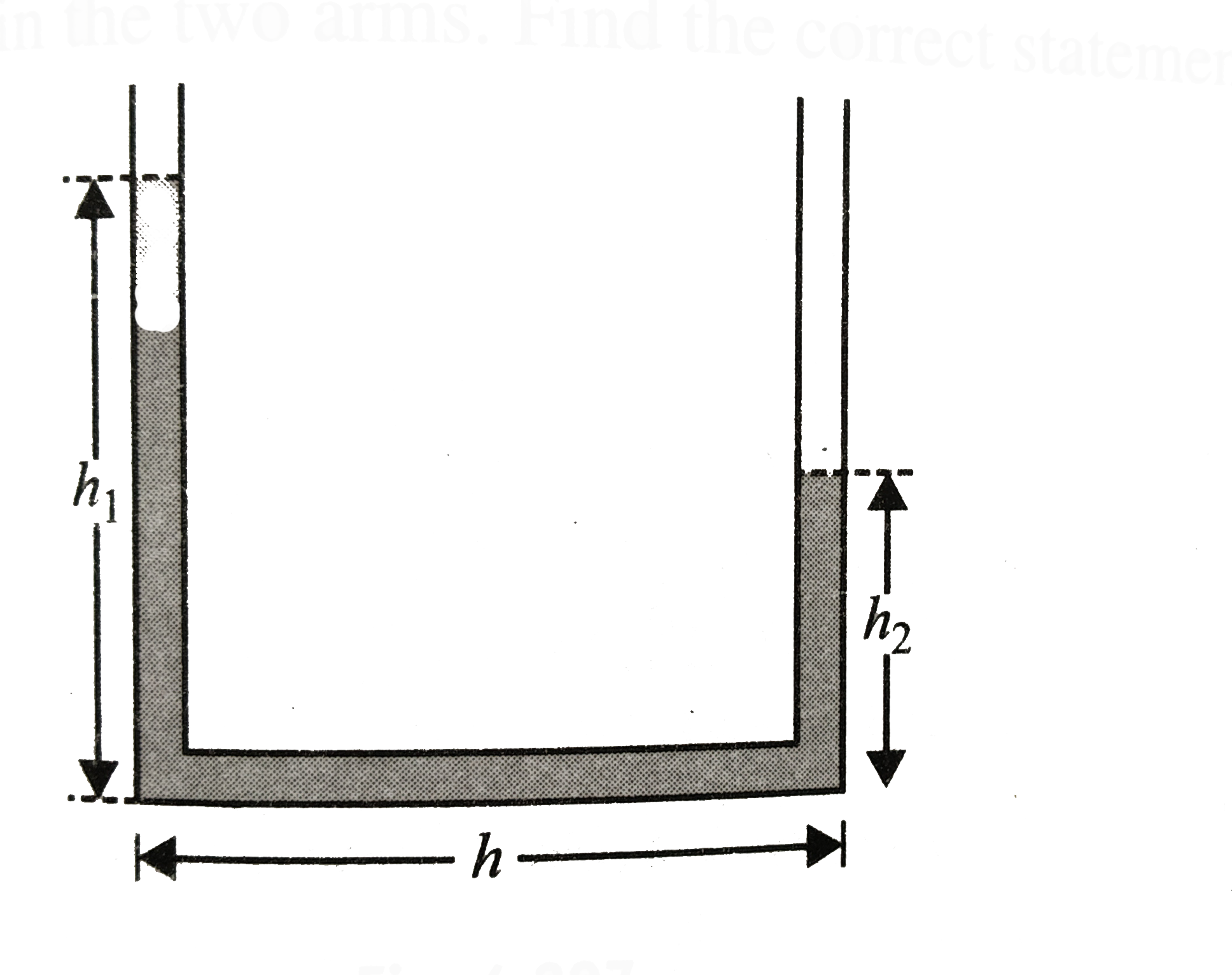
View SolutionThe U-tube shown in the figure has a uniform cross section. A liquid is filled up to heights h1 and h2 in the two arms and they are allowed to move. Neglecting viscosity and surface tension, find the state of the liquid when the levels equalize in the two arms. Find the correct statement.
View Solution
