
A rough vertical board has an acceleration so that a 2 kg block pressing against it dows not fall. The coefficient of friction between the block and the board should be
The correct Answer is:A
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - IV35videos
LAW OF MOTION
- BOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (H.W)(CIRCULAR MOTION)3videos
LAW OF MOTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
- BOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q13videos
MATHEMATICAL REVIEW & PHYSICAL WORLD
Similar Questions
A block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
View SolutionA block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
View Solution
Knowledge Check
- Question 1 - Select One
A horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
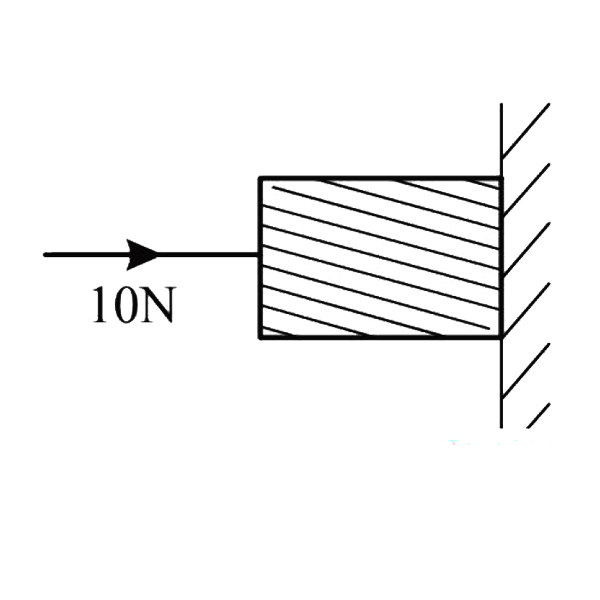 A(a) 20NB(b) 50NC(c) 100ND(d) 2N
A(a) 20NB(b) 50NC(c) 100ND(d) 2N - Question 2 - Select One
A horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
 A20 NB50 NC100 ND2 N
A20 NB50 NC100 ND2 N - Question 3 - Select One
A block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, what is the minimum force required to be applied by the finger to hold the block against the wall?
AμMgBMgCMgμD2μMg
A block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
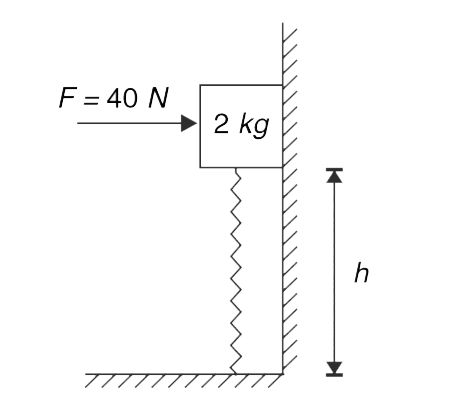
View Solution(i) In the arrangement shown in the figure the coefficient of friction between the 2 kg block and the vertical wall is μ=0.5. A constant horizontal force of 40 N keeps the block pressed against the wall. The spring has a natural length of 1.0 m and its force constant is k=400Nm–1. What should be the height h of the block above the horizontal floor for it to be in equilibrium. The spring is not tied to the block.
(ii) A block of mass M is pressed against a rough vertical wall by applying a force F making an angle of θ with horizontal (as shown in figure). Coefficient of friction between the wall and the block is μ=0.75.
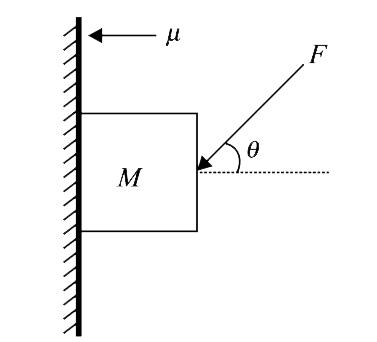
(a) If F = 2 Mg, find the range of values of θ so that the block does not slide
[Take tan37∘=0.75,sin24∘=0.4]
(b) Find the maximum value of θ above which equilibrium is not possible for any magnitude of force F.View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View Solution
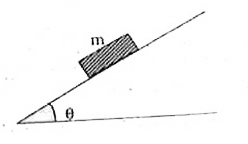
A board is moving with velocity v on a smoother horizontal plane. The upper surface of the board is rough on which a ball falls with velocity v and rebounds with velocity v2. The mass of the board is same as that of ball. After the collision, the board comes to state of rest. The co-efficient of friction between the board and the ball isView SolutionIn the given system, a block of mass m is resting on a board which makes an angle θ with the horizontal. What should be the minimum value of θ, so that the block just starts moving downwards? The coefficient of friction between the surfaces of the board and the block is μ.
 View Solution
View Solution

