A body of mass M and radius R is rolling horizontally without slipping with speed v . It then rolls up a hill to a maximum height h . If h=5v26g , what is the M.I of the body ?
MR22
23MR2
34Mr2
25MR2
The correct Answer is:B
To solve the problem, we will use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the initial conditions
The body of mass M and radius R is rolling without slipping with an initial speed v. The body has both translational and rotational kinetic energy.
Step 2: Write the expression for initial kinetic energy
The total initial kinetic energy KEinitial of the body can be expressed as the sum of translational kinetic energy and rotational kinetic energy:
KEinitial=KEtranslational+KErotational=12Mv2+12Iω2
Where I is the moment of inertia and ω is the angular velocity.
Step 3: Relate angular velocity to linear velocity
For a body rolling without slipping, the relationship between linear velocity v and angular velocity ω is given by:
ω=vR
Substituting this into the rotational kinetic energy term:
KErotational=12I(vR)2=Iv22R2
Step 4: Substitute into the kinetic energy equation
Now, substituting KErotational back into the total kinetic energy:
KEinitial=12Mv2+Iv22R2
Step 5: Write the expression for potential energy at height h
When the body rolls up to a height h, its kinetic energy is converted into gravitational potential energy PE:
PE=Mgh
Given that h=5v26g, we can substitute this into the potential energy equation:
PE=Mg(5v26g)=5Mv26
Step 6: Apply the conservation of energy principle
According to the conservation of energy:
KEinitial=PE
Substituting the expressions we derived:
12Mv2+Iv22R2=5Mv26
Step 7: Simplify the equation
To simplify, we can multiply through by 6R2 to eliminate the fractions:
3Mv2R2+3Iv2=5Mv2R2
Now, rearranging gives:
3Iv2=5Mv2R2−3Mv2R2
3Iv2=2Mv2R2
Dividing both sides by v2 (assuming v≠0):
3I=2MR2
Step 8: Solve for the moment of inertia I
Finally, solving for I:
I=2MR23
Final Answer
The moment of inertia of the body is:
I=2MR23
---
The body of mass M and radius R is rolling without slipping with an initial speed v. The body has both translational and rotational kinetic energy.
The total initial kinetic energy KEinitial of the body can be expressed as the sum of translational kinetic energy and rotational kinetic energy:
KEinitial=KEtranslational+KErotational=12Mv2+12Iω2
Where I is the moment of inertia and ω is the angular velocity.
For a body rolling without slipping, the relationship between linear velocity v and angular velocity ω is given by:
ω=vR
Substituting this into the rotational kinetic energy term:
KErotational=12I(vR)2=Iv22R2
Now, substituting KErotational back into the total kinetic energy:
KEinitial=12Mv2+Iv22R2
When the body rolls up to a height h, its kinetic energy is converted into gravitational potential energy PE:
PE=Mgh
Given that h=5v26g, we can substitute this into the potential energy equation:
PE=Mg(5v26g)=5Mv26
According to the conservation of energy:
KEinitial=PE
Substituting the expressions we derived:
12Mv2+Iv22R2=5Mv26
To simplify, we can multiply through by 6R2 to eliminate the fractions:
3Mv2R2+3Iv2=5Mv2R2
Now, rearranging gives:
3Iv2=5Mv2R2−3Mv2R2
3Iv2=2Mv2R2
Dividing both sides by v2 (assuming v≠0):
3I=2MR2
Finally, solving for I:
I=2MR23
The moment of inertia of the body is:
I=2MR23
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - C.U.Q71videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - I (C.W)63videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 34videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)19videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A body of mass M and radius r, rolling on a smooth horizontal floor with velocity v, rolls up an irregular inclined plane up to a vertical height (3v2/4g). Compute the moment of inertia of the body.
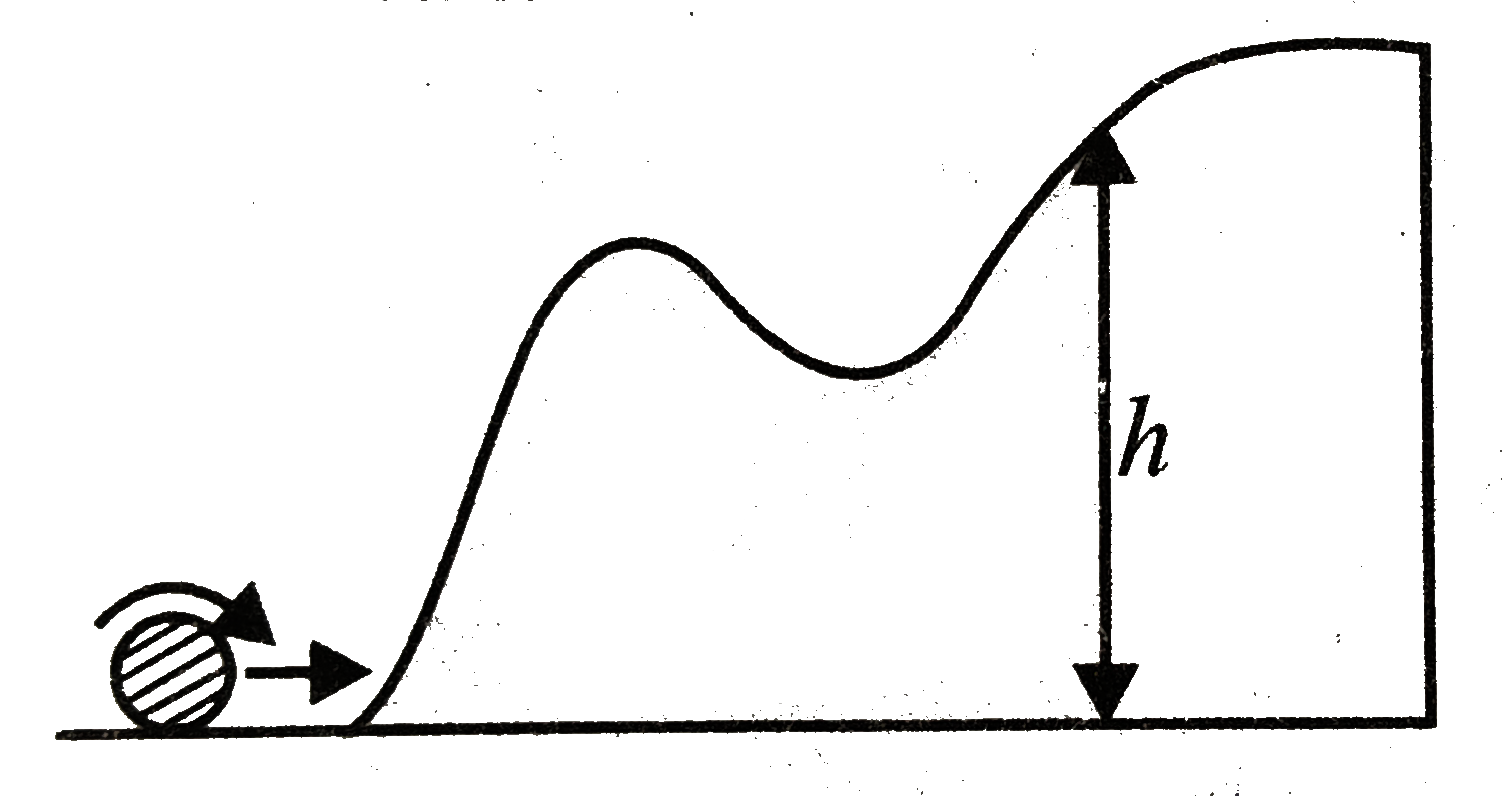 View Solution
View SolutionA body of radius R and mass m is rolling smoothly with speed v on a horizontal surface. It then rolls up a hill to a maximum height h. If h=3v2/4g. What might the body be ?
View Solution
Knowledge Check
- Question 1 - Select One
An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
Asolid sphereBhollow sphereCdiscDring - Question 2 - Select One
An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
A25MR2BMR22CMR2D32MR2 - Question 3 - Select One
A mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
Athe body is identified to be a disc or a solid cylinderBthe body is a solid sphereCmoment of inertia of the body about instantaneous axis of rotation is 32mr2Dmoment of inertial of the body about instantaneous axis of rotation is 75mr2
A sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with the speed u . Now if it rolls up vertically , the maximum height it would attain will be
View SolutionA disc of radius R and mass M is rolling horizontally without slipping with speed with speed v. It then moves up an incline as shown in figure. The maximum height upto which it can reach is.
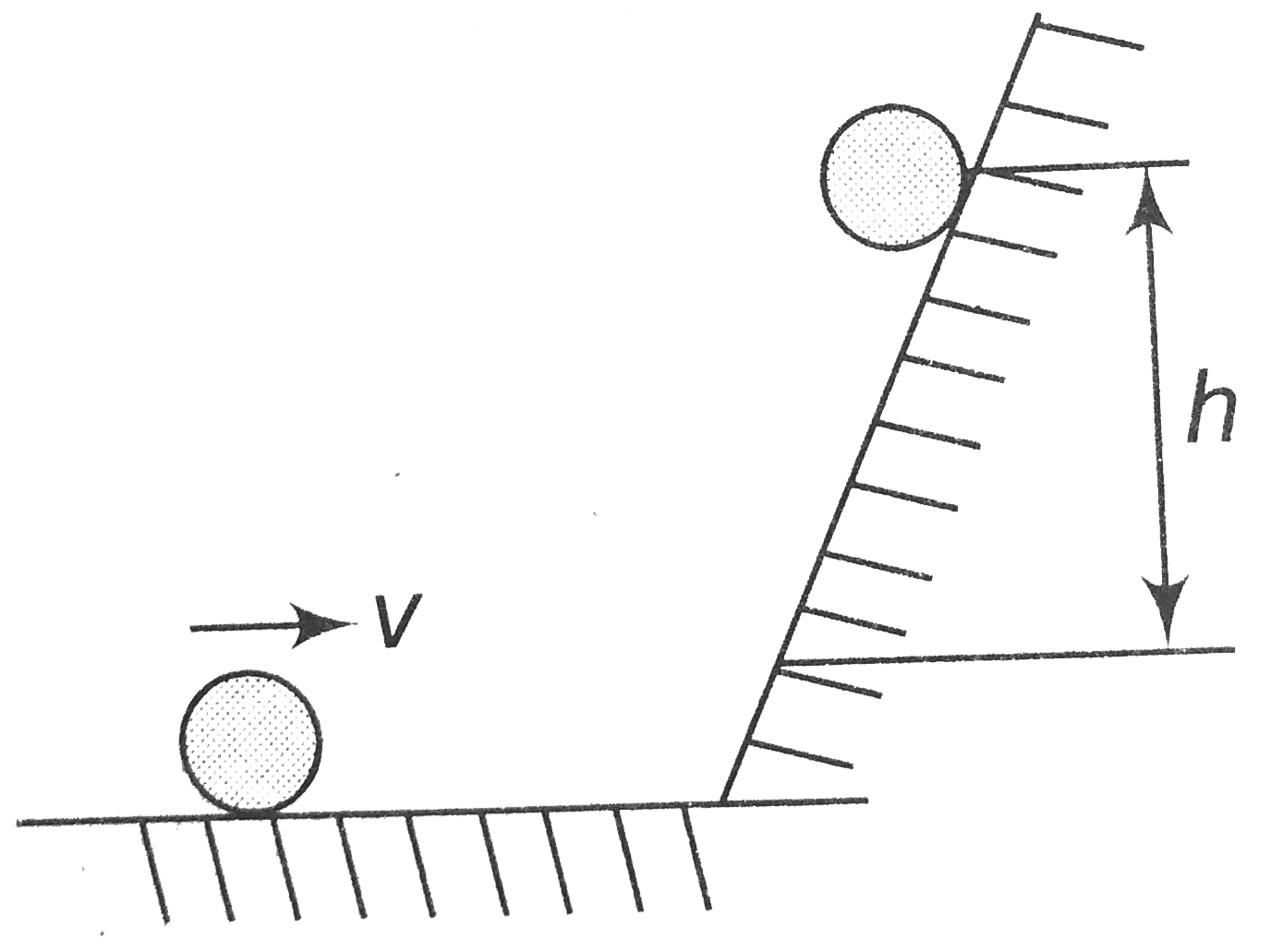 .View Solution
.View SolutionA loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
View SolutionA symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
View Solution

