A heavy wheel of radius 20cm and weight 10kg is to be dragged over a step of height 10cm, by a horizontal force F applied at the centre of the wheel. The minimum value of F is
20kgwt
1kgwt
10√3kgwt
10√2kgwt
The correct Answer is:C
clockwise torque = anticlockwise torque : mg√(20)2−(10)2=F(20−10)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - III
Explore 43 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - II (C.W)
Explore 60 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
As shown, a wheel of weight W and radius 1.0m is placed against a 0.4m height rectangular block fixed on the ground. The wheel has an axle of radius 0.1m. A force F is applied tangentially to the axle to lift the wheel. The minimum value of F is given.by expression F=αW11. Then find the value of α.
'(##CEN_KSR_PHY_JEE_C09_E01_039_Q21##)'
View SolutionThe minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2
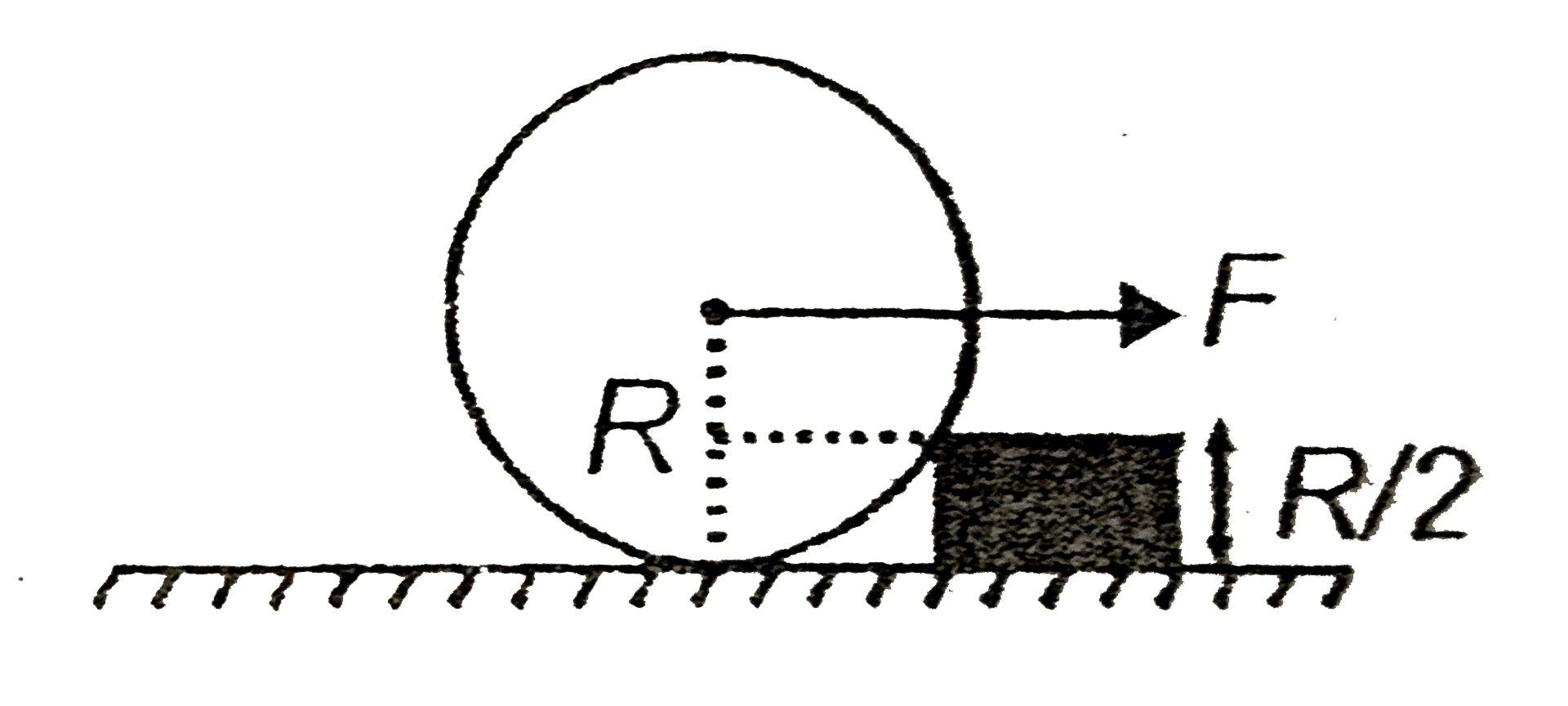
View Solution
Knowledge Check
A wheel of radius r and mass m stands in front of a step of height h. The least horizontal force which should be applied to the axle of the wheel to allow it to raise onto the step is
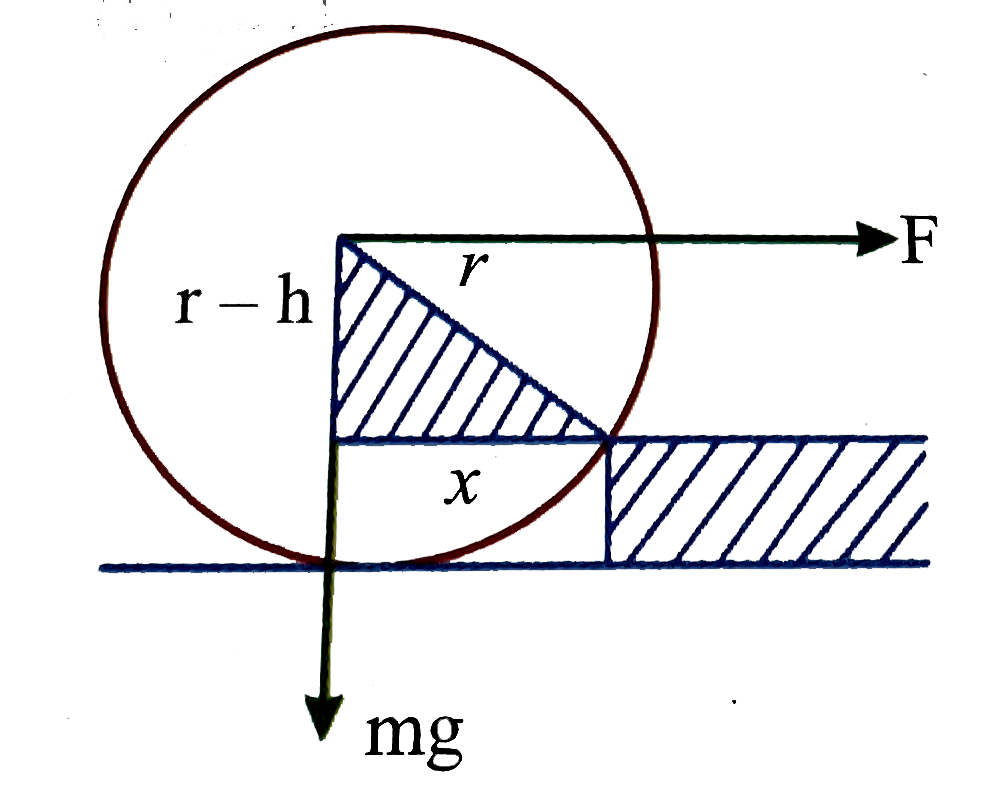 Amgh(2r−h)r−hBmgh(r−h)Cmg(√h(2r−h))r−hDmghr
Amgh(2r−h)r−hBmgh(r−h)Cmg(√h(2r−h))r−hDmghrA roller of mass 300kg and of radius 50cm lying on horizontal floor is resting against a step of height 20cm. The minimum horizontal force to be applied on the roller passing through its centre to turn the roller on to the step is
A980NB1960NC2940ND3920NA vertical disc of mass 5kg and radius 50cm rests against a steo of height 25cm as shown in figure. What minimum horizontal force applied perpendicular to the axle will make the disc to climb the step ? Take g=10m/s2.
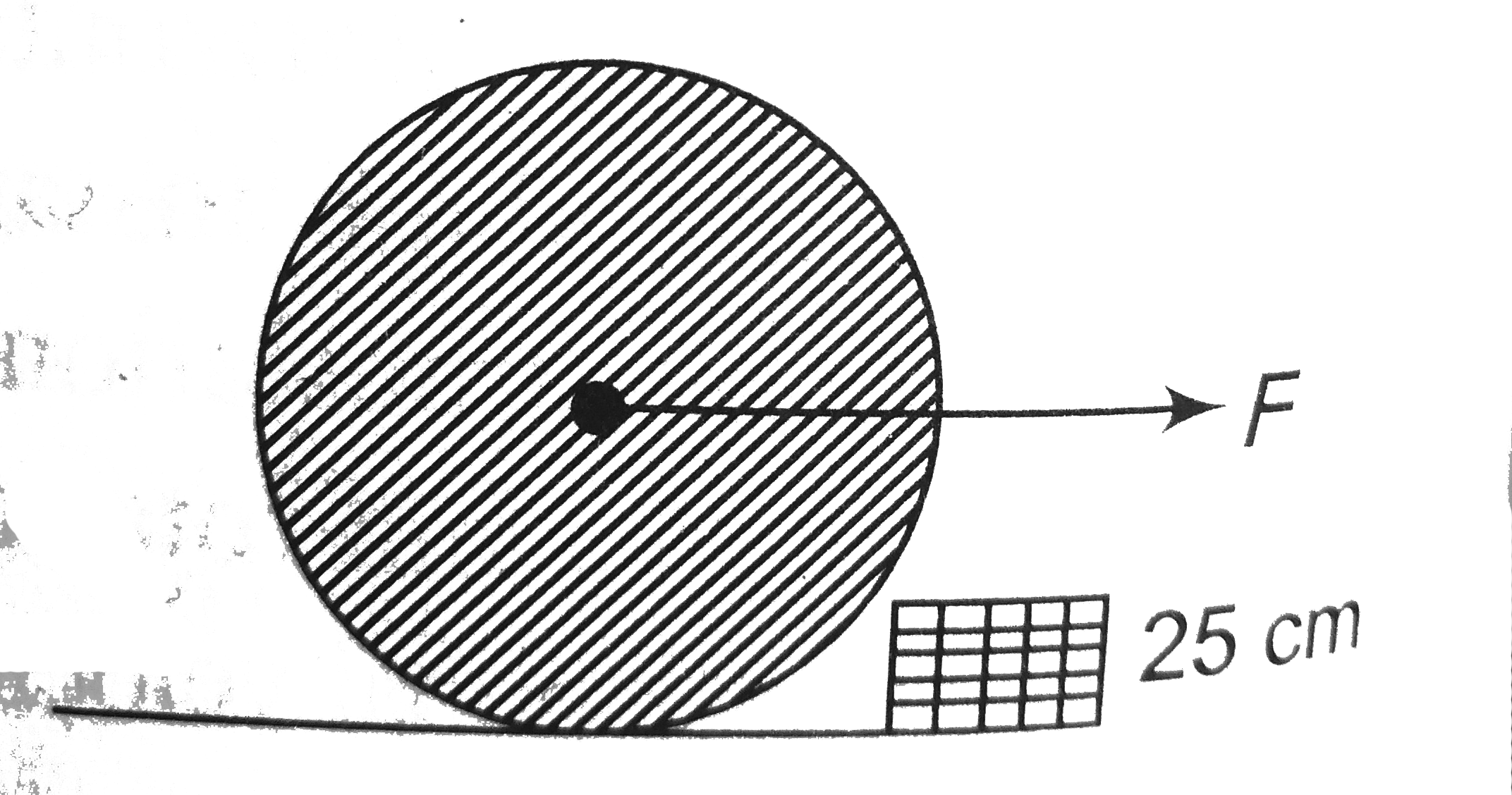 .A50 NB50√3NC25NDnone of these
.A50 NB50√3NC25NDnone of these
A cuboid of height 10 cm, width 5 cm and 8 kg is kept on a rough horizontal ground as shown . The ground is so rough that we can assume that the questions indicated below. A boy applies a horizontal force F at the top edge of the cuboid.

What is the minimum value of F so taht the block begins to topple ?
View SolutionA uniform cylinder of mass M and radius R is to be pulled over a step of height a (a<R) by applying a force F at its centre O perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure ) . The minimum value of F required is :
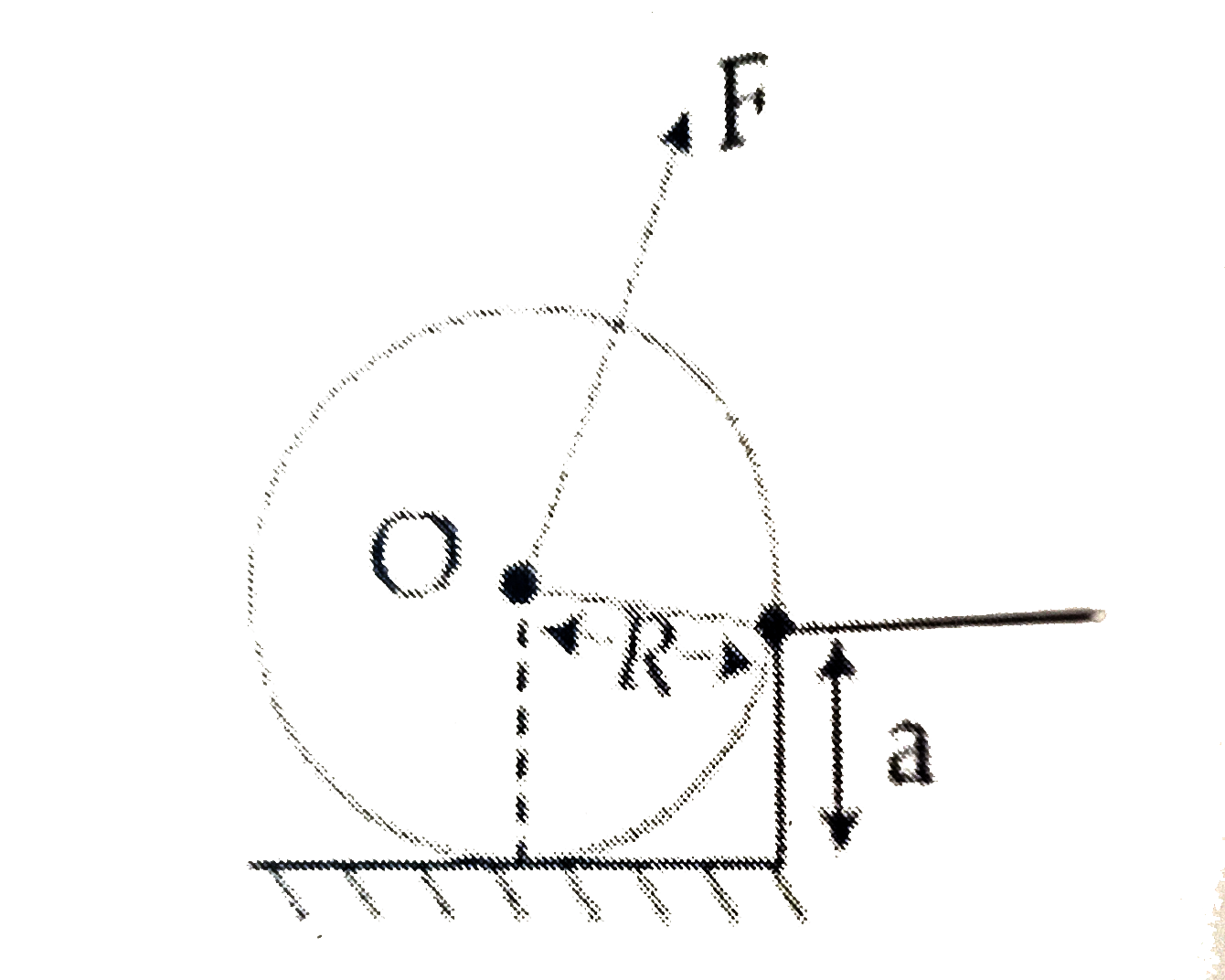
View SolutionWhich has more volume a cylinder of radius 10 cm and height 25 cm or 25 cm and height 10 cm?
View SolutionThe drwing shows a bicycle wheel of radius r, resting against a small step whose height is h=r/5. A clockwise torque increases, there comes a time when the wheel just begins to rise up and loses contact with the ground. Let this torque be T. What is the magniitude of the horizontal component of the acceleration of the centre of the wheel when a torque of 2T is applied? Assume that the wheel doesn't slip at the edge of the step when this torque is applied (ignore the mass of the spokes).

View SolutionA wheel of radius R has an axle of radius R/5. A force F is applied tangentially to the wheel. To keep the system in a state of "rotational" rest, a force F' is applied tangentially to the axle. The value of F' is
View Solution