A wheel having radius 10 cm is coupled by a belt to another wheel of radius 30 cm . 1st wheel increases its angular speed from rest at a uniform rate of 1.5rads−2 . The time for 2nd wheel to reach a rotational speed of 100rev/min is ... (assume that the belt does not slip )
20 sec
10 sec
1.5 sec
15sec
The correct Answer is:A
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given values
- Radius of the first wheel, r1=10cm=0.1m
- Radius of the second wheel, r2=30cm=0.3m
- Angular acceleration of the first wheel, α1=1.5rad/s2
- Final rotational speed of the second wheel, ω2=100rev/min
Step 2: Convert the final speed of the second wheel to radians per second
To convert revolutions per minute to radians per second, we use the conversion factor:
ω2=100rev/min×2πrad1rev×1min60s=100×2π60rad/s=10π3rad/s
Step 3: Relate the angular velocities of the two wheels
Since the belt does not slip, the linear velocities at the edges of both wheels must be equal:
v1=v2
This can be expressed in terms of angular velocities:
r1ω1=r2ω2
Where ω1 is the angular velocity of the first wheel. Rearranging gives:
ω1=r2r1ω2
Substituting the known values:
ω1=0.30.1⋅10π3=3⋅10π3=10πrad/s
Step 4: Use the angular acceleration to find the time taken
The angular velocity of the first wheel starts from rest, so we can use the equation:
ω1=ω01+α1t
Where ω01=0 (initial angular velocity). Thus:
10π=0+1.5t
Solving for t:
t=10π1.5=20π3≈20.94s
Step 5: Conclusion
The time taken for the second wheel to reach a rotational speed of 100 rev/min is approximately 20.94s.
- Radius of the first wheel, r1=10cm=0.1m
- Radius of the second wheel, r2=30cm=0.3m
- Angular acceleration of the first wheel, α1=1.5rad/s2
- Final rotational speed of the second wheel, ω2=100rev/min
To convert revolutions per minute to radians per second, we use the conversion factor:
ω2=100rev/min×2πrad1rev×1min60s=100×2π60rad/s=10π3rad/s
Since the belt does not slip, the linear velocities at the edges of both wheels must be equal:
v1=v2
This can be expressed in terms of angular velocities:
r1ω1=r2ω2
Where ω1 is the angular velocity of the first wheel. Rearranging gives:
ω1=r2r1ω2
Substituting the known values:
ω1=0.30.1⋅10π3=3⋅10π3=10πrad/s
The angular velocity of the first wheel starts from rest, so we can use the equation:
ω1=ω01+α1t
Where ω01=0 (initial angular velocity). Thus:
10π=0+1.5t
Solving for t:
t=10π1.5=20π3≈20.94s
The time taken for the second wheel to reach a rotational speed of 100 rev/min is approximately 20.94s.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - III
Explore 43 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - II (C.W)
Explore 60 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
In Fig. 10-54, wheel A of radius rA=10cm is coupled by belt B to wheel C of radius rC=25cm. The angular speed of wheel A is increased from rest at a constant rate of 2.0rad/s2. Find the time needed for wheel C to reach an angular speed of 100 rev/min, assuming the belt does not slip.

View SolutionWheel A of radius rA=10cm is coupled by a belt C to another wheel of radius rB=25cm as in the figure. The wheels are free to rotate and the belt does not slip . At time t=0 wheel A increases it's angular speed from rest at a uniform rate π/2rad/sec2 Find the time in which wheel B attains a speed of 100r±[ Hint :vA=vB]

View Solution
Knowledge Check
In figure whell A of radius rA=10cm is coupled by belt B to whell C of radius rC=25cm. The angular speed of whell A is increased from rest at a constant rate of 1.6rad/s2. Find the time needed for whell C to reach an angular speed of 12.8rad/s, assuming the belt does not slip.
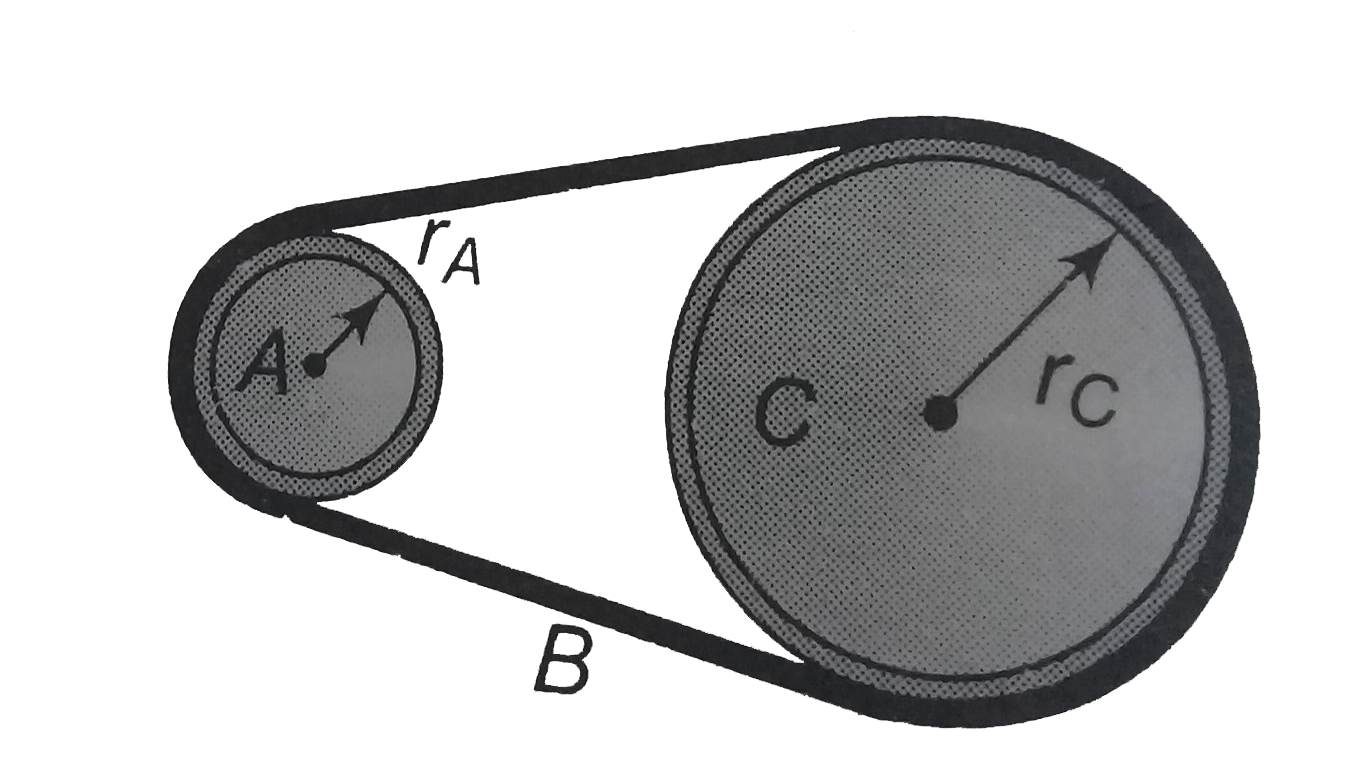 .A15 sB12.5 sC20 sD10 s
.A15 sB12.5 sC20 sD10 sA wheel covers a distance of 1,100 cm in one round. The radius of the wheel is:
एक पहिया एक चक्कर में 1,100 सेमी की दूरी तय करता है | इस पहिये का व्यास कितना है ?A125 cmB100 cmC350 cmD150 cmA wheel covers a distance of 1,100 cm in one round. The radius of the wheel is :
A100 cmB175 cmC125 cmD150 cm
Two wheels having radii in the ratio 1:3 are connected by a common belt. If the smaller wheel is accelerated from rest at a rate 1.5rads2 for 10 s, find the angular velocity of bigger wheel
View SolutionA wheel starting from rest,rotates with a uniform angular acceleration of 2rads2 .Then the number of rotations it performs in tenth second is
View SolutionA wheel of radius 15cm is rotating about its axis at angluar speed of 20rad/s. Find the linear speed and total acceleration of a point on the rim.
View SolutionA wheel is rotating about a its own axis. The moment of inertia of the wheel about axis of rotation.If its angular speed is 30 rad/sec and its kinetic energy is 300J ( in kg−m2)
View SolutionA belt passes over a wheel of radius 25 cm. If a point on the belt has a speed of 5m/s, the belt is moving with an angular velocity of
View Solution
