Point a rod b ( l = 2m) is moved upwards against a wall with velocity v = 2 m/s . Find angular speed of the rod at an instant when θ=60∘

4rad/s
1.155rad/s
2rad/s
2.50rad/s
The correct Answer is:C
ω=vLcosθ
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - III
43 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - II (C.W)
60 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
There is a fixed half cylinder of radius R on a horizontal table. A uniform rod of length 2R leans against it as shown. At the instant shown, θ=30∘ and the right end of the rod is sliding with velocity v.
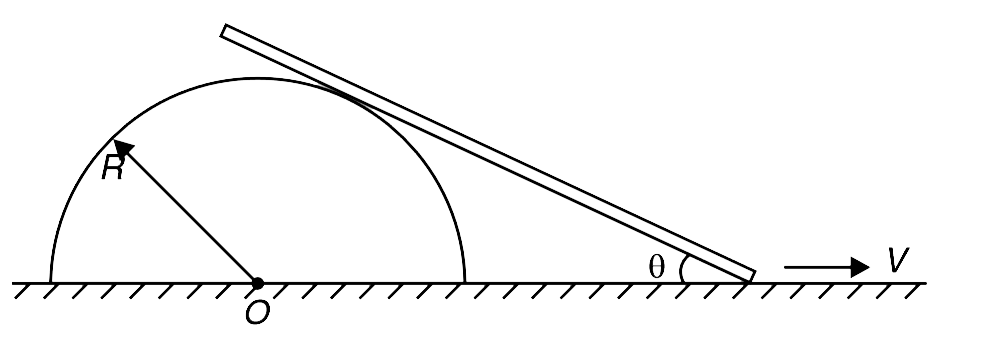
(a) Calculate the angular speed of the rod at this instant.
(b) Find the vertical component of the velocity of the centre of the rod at this instant.
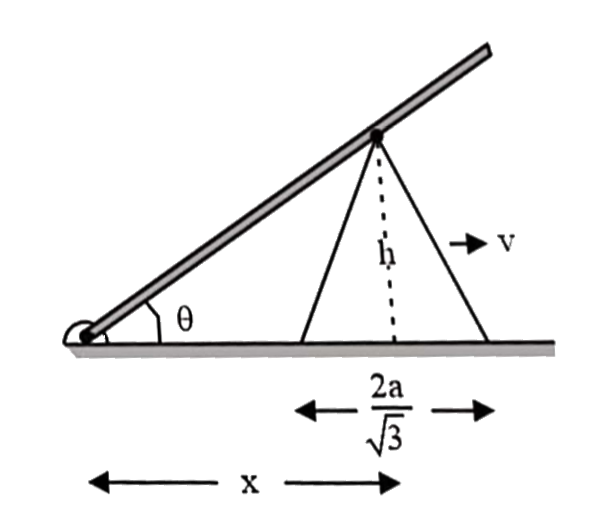
View SolutionIn the given arrangement, the rod is free to rotate about the hinge and it is in constant contact with the equilateral triangular block of base length 2a√3. If the block is moving horizontally with a speed υ=20ms−1, then find the magnitude of the angular velocity of the rod (in rad. s−1)at the instant when θ=30∘. [Given that a=1m]
View Solution
Knowledge Check
Point A of rod AB(l=2m) is moved upwards against a wall with velocity v=2m/s. Find angular speed of the rod at an instant when θ=60∘.
 A4rad/sB1.155rad/sC2rad/sD2.50rad/s
A4rad/sB1.155rad/sC2rad/sD2.50rad/sA rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
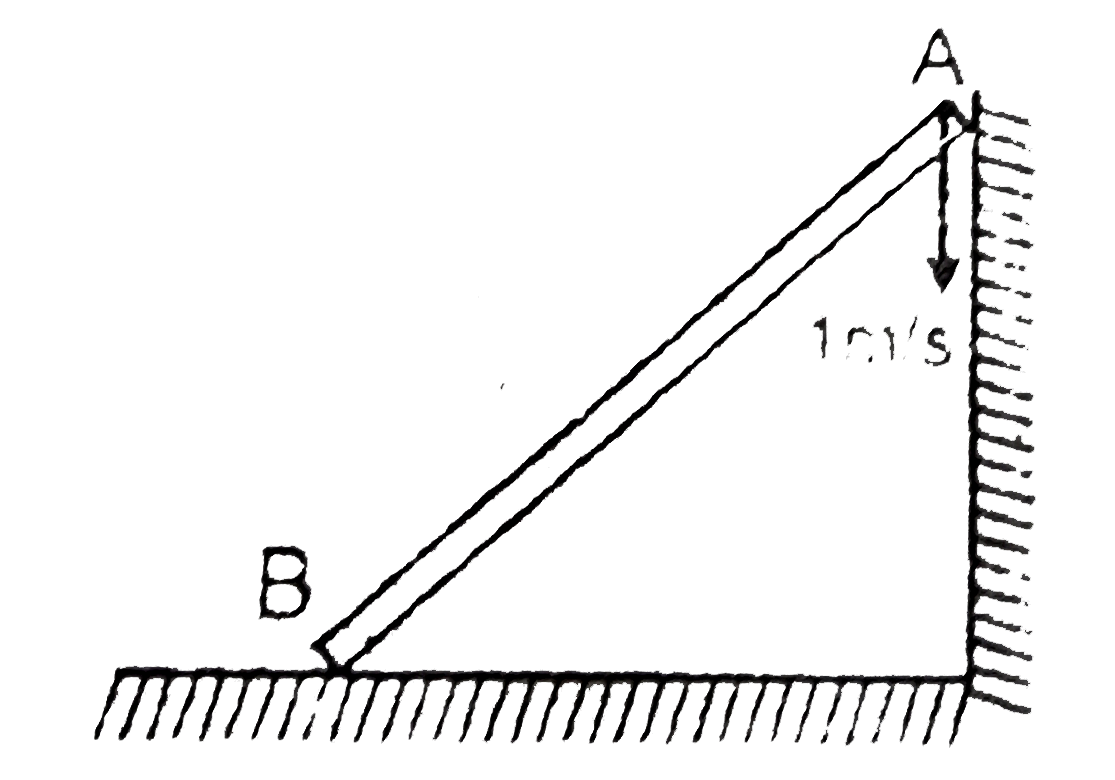 A2 rad/sB1.5 rad/sC0.5 rad/sD0.75 rad/s
A2 rad/sB1.5 rad/sC0.5 rad/sD0.75 rad/s
In the given arrangement, the rod is free to rotate about the hinge and it is in constant contact with the equilateral triangular block of base length 2a√3. If the block is moving horizontally with a speed υ=20ms−1, then find the magnitude of the angular velocity of the rod (in rad. s−1)at the instant when θ=30∘. [Given that a=1m]

View SolutionThe end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘
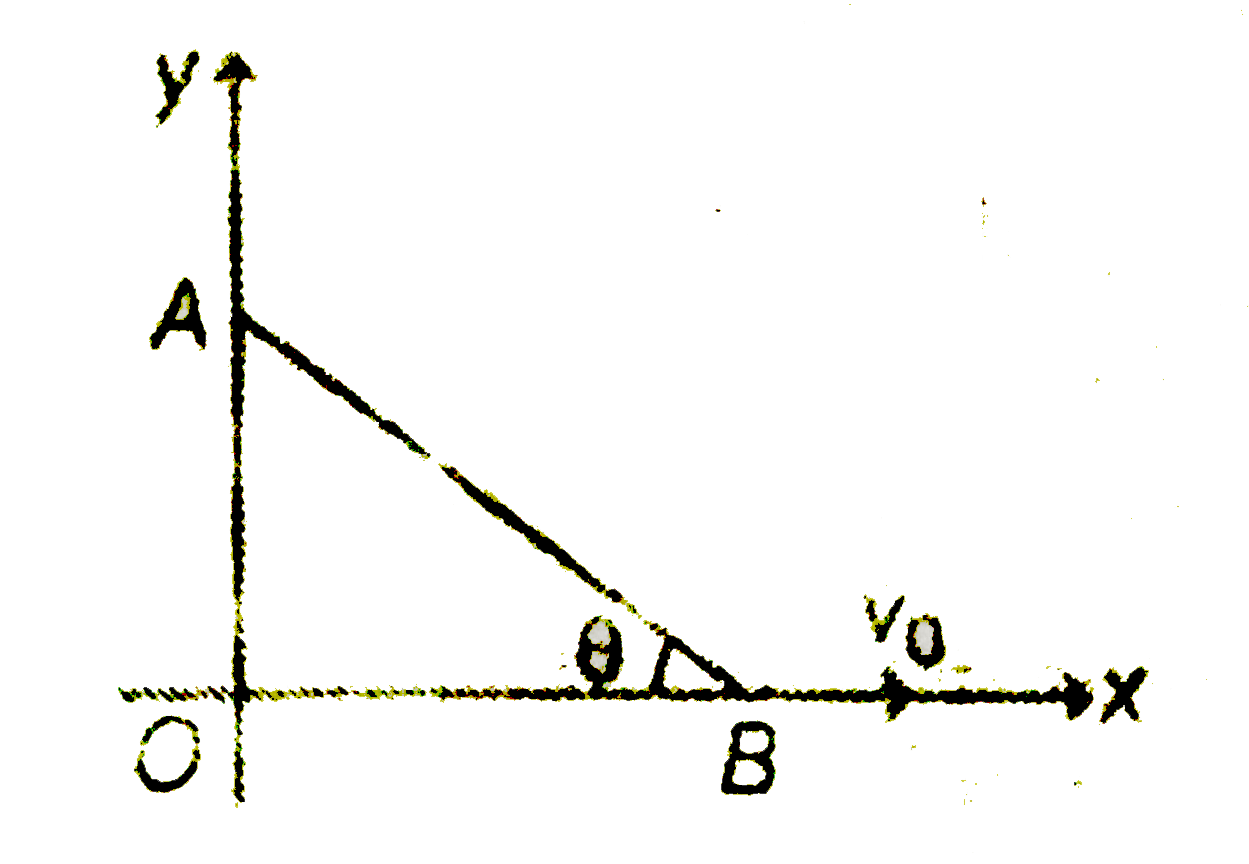
(A)velocity of end A is 43v0 downwards
(B)angular velocity of rod is 53v0l
(C)angular velocity of rod is constant
(D)velocity of end A is constant
View SolutionA rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :

View SolutionA rod of length l is moving in a vertical plane (x−y) when the lowest point A of the rod is moved with a velocity v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionA uniform rod of mass M and length l is hinged at point O and is free to rotate on a horizontal smooth surface. Point O is at a distance of l4 from one end of the rod. A sharp impulse P0=2√130kgm/s is applied along the surface at one end of the rod as shown in figure [tanθ=97]
(a) Find the angular speed of the rod immediately after the hit
(b) Find the impulse on the rod due to the hinge.

View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View Solution
