The moment of inertia of a wheel of radius 20cm is 40kgm2 if a tangential force of 80N applied on the wheel, its rotational K.E. after 4s is
16.2 J
51.2 J
25.6 J
24.8 J
The correct Answer is:B
ω=ω0+αt.KE=12Iω2
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - III43videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - II (C.W)60videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)19videos
THERMAL PROPERTIES OF MATTER
Similar Questions
The moment of inertia of a wheel of radius 10cm is 20kgm2 ,If a tangential force of 40N applied on the wheel,its Rotational K.E.after 2s is ?
View SolutionThe moment of inertia of a wheel is 1000kg−m2. At a given instant, its angular velocity is 10rad/s. After the wheel rotates through an angle of 100 radians the wheel's angular velocity is 100rad/s. Find the torque applied on wheel.
View Solution
Knowledge Check
- Question 1 - Select One
The moment of inertia of a solid flywheel about its axis is 0.1kg−m2.A tangential force of 2 kg-wt. is applied round the circumference of the flywheel with the help of a string and mass arrangement as shown in the figure. If the radius of the wheel is 0.1 m, find the acceleration (in rad/sec2) of the mass :
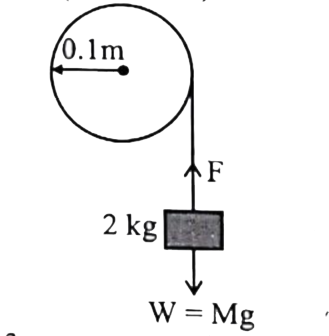 A163.3B16.3C81.66D8.16
A163.3B16.3C81.66D8.16 - Question 2 - Select One
A wheel of mass 5kg and radius 0.40m is rolling on a road without sliding with angular velocity 10rads−1. The moment of ineria of the wheel about the axis of rotation is 0.65kgm2. The percentage of kinetic energy of rotate in the total kinetic energy of the wheel is.
A22.4%B11.2%C88.8%D44.8% - Question 3 - Select One
A flywheel of moment of inertia 2kg-m2 is rotated at a speed of 30rad/s. A tangential force at the rim stops the wheel in 15 second. Average torque of the force is
A4 N-mB2 N-mC8 N-mD1 N-m
Compute the angular acceleration of a wheel having moment of inertia 20kgm2, when a torque of 10Nm is applied on the wheel.
View SolutionConsider the situation as shown in the figure. The moment of inertia of wheel is 2kgm2 and its radius is 0.25m. Find the angular acceleration of the wheel, assuming no slipping.
 View Solution
View SolutionA wheel is rotating at a speed of 1000 rpm and its KEis106J. What is moment of inertia of the wheel about its axis of rotation ?
View SolutionThe moment of inertia of a disc rotating about an axis passing through its centre and perpendicular to its axis is 20kgm2 . If its rotational K.E. is 10 J, then its angular momentum will be
View SolutionA wheel 2 kg having practically all the mass concentrated along the circumference of a circle of radius 20 cm is rotating on its axis with angular velocity of 100 rad/s, then the rotational kinetic energy of wheel is
View Solution

