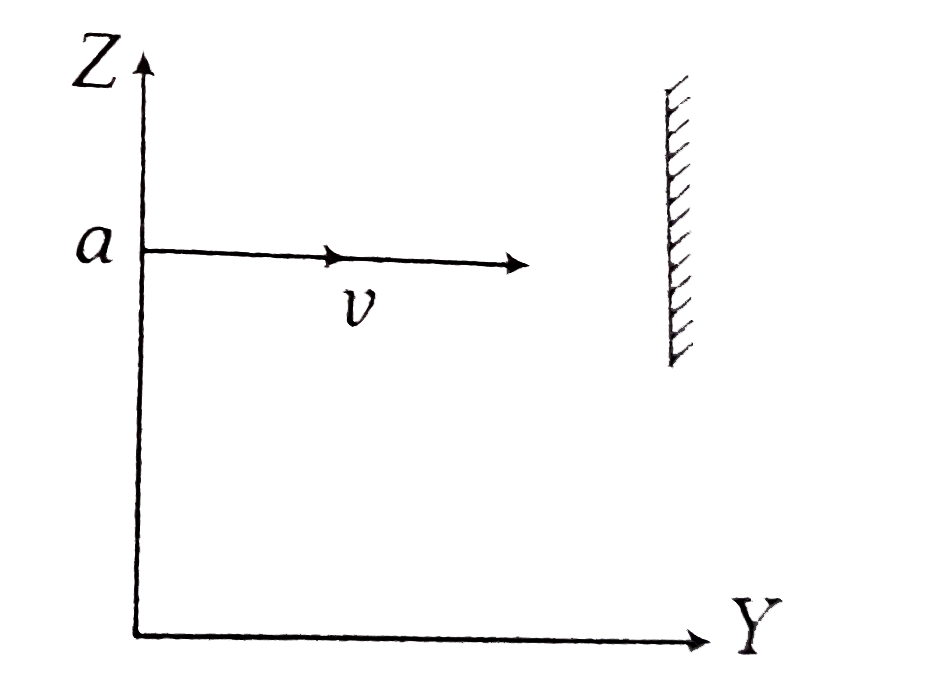
A particle of mass m is moving in yz - plane with a uniform veloci

A particle of mass $m$ is moving in yz-plane with a unifrom velocity $v$ with its trajectory running parallel to +ve y-axis and intersecting z-axis at $z = a$ Fig. The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is :

A $m v a {ˆ e}_{x}$
B $2 m v a {ˆ e}_{x}$
C $y m v a {ˆ e}_{x}$
D $2 y m v a {ˆ e}_{x}$
A particle of mass m is moving with a uniform velocity $v_{1}$ . It is given an impulse such that its velocity becomes $v_{2}$ . The impulse is equal to
A $m (v_{1} + v_{2})$
B $m [| v_{2} | - | v_{1} |]$
C $\frac{1}{2} (v_{2}^{2} - v_{1}^{2})$
D $m (v_{2} - v_{1})$
A particle of mass m is moving with a uniform velocity $v_{1}$ . It is given an impulse such that its velocity becomes $v_{2}$ . The impulse is equal to
A $m [| v_{2} | - | v_{1} |]$
B $\frac{1}{2} m (v_{2}^{2} - v_{1}^{2})$
C $m (v_{1} + v_{2})$
D $m (v_{2} - v_{1})$

The correct Answer is:B