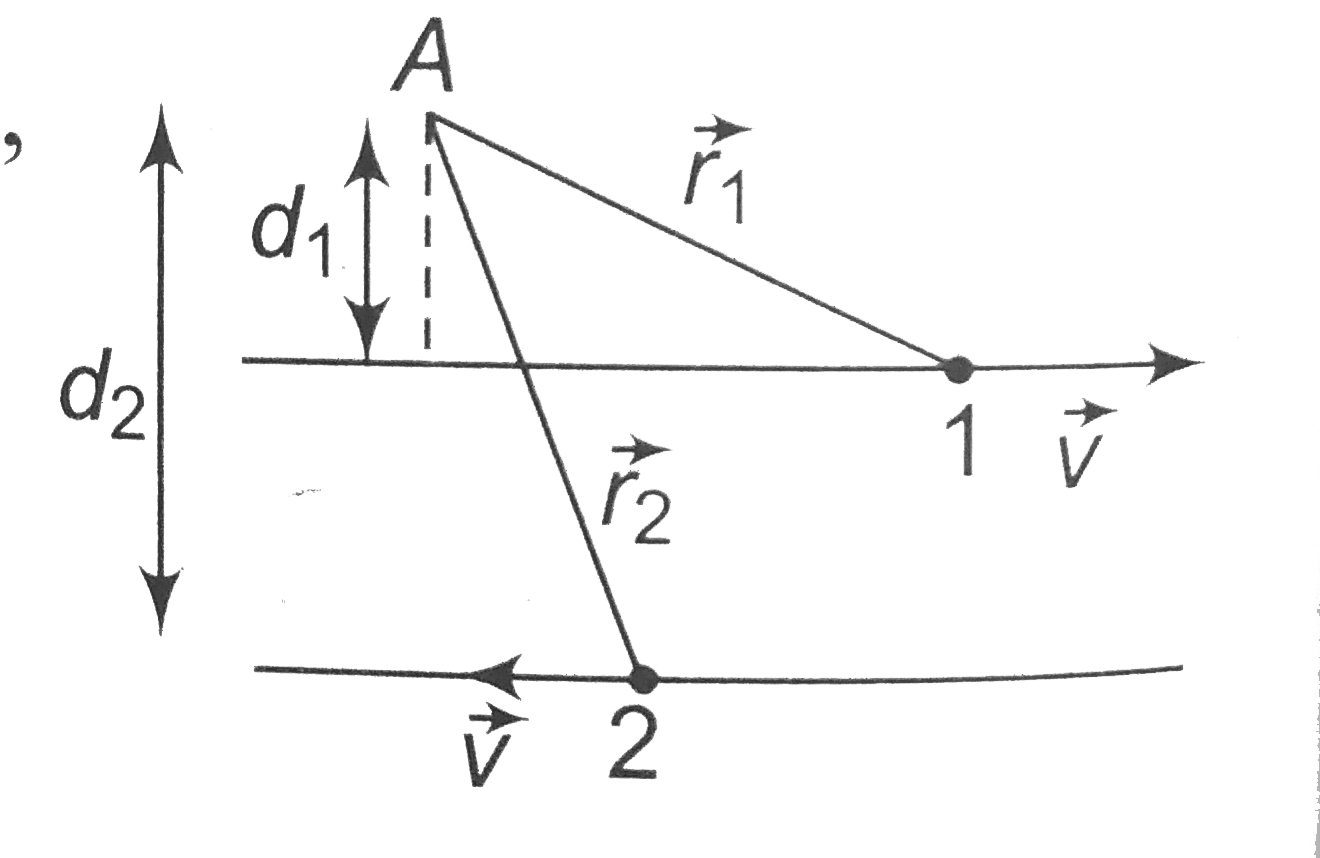
Figure shows two identical particles 1 and 2 , each of mass m . Moving in opposite directions with same speed v along parallel lines . At a particular instant , r1andr2 are their respective position vectors drawn from point which is in plane of the parallel lines . Choose the correct option :

Angular momentum I1 of particle 1 about A is I1=mv1d1⊗
Angular momentum I2 of particle 2 about A is I2=mvr2⊙
Total angular momentum of the system about A is I=mv(r1+r2)⊙
Total angular momentum of the system about A is I=mv(d2−d1)⊗
The correct Answer is:D
Conceptual
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - III
43 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
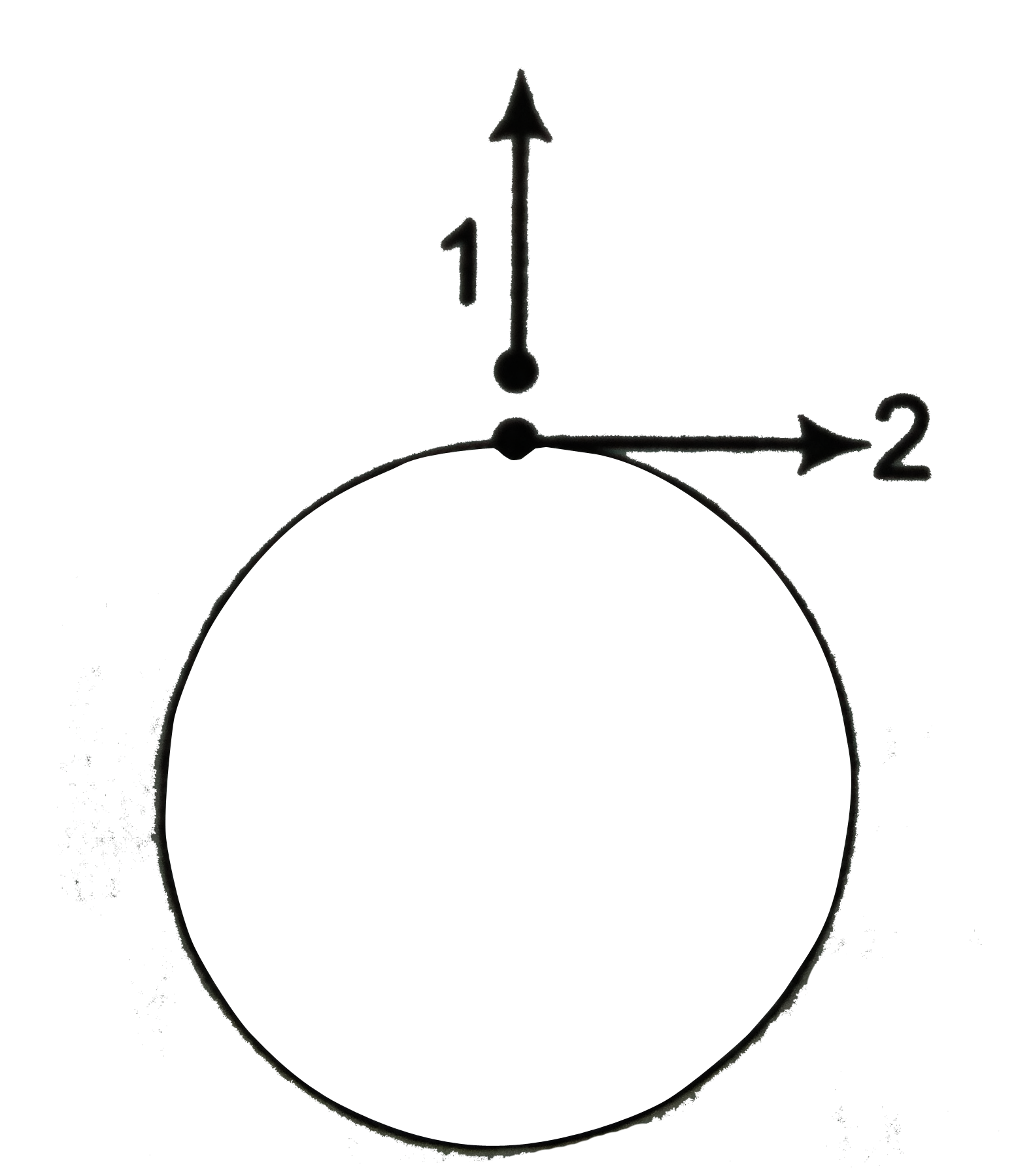
Two identical particles 1 and 2 are projected from surface of earth with same velocities in the directions shows in figure.
View SolutionTwo particles each of mass m and speed v, travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.
View Solution
Knowledge Check
Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed →V along parallel lines. At a particular instant, →r1 and →r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Which of the following is the correct statement ?
 .AAngular momentum →L1 of particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
.AAngular momentum →L1 of particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
[Here, ⊗ represents a unit vector going into the page and ⊙ represents a unit vector coming out of the page].Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed →V along parallel lines. At a particular instant, →r1 and →r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Which of the following is the correct statement ?
 .AAngular momentum →L1 of a particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about A is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
.AAngular momentum →L1 of a particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about A is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
⊗ represents a unit vector going into the page, ⊙ represent a unit vector coming out of the pageTwo identical particles 1 and 2 are projected from surface of earth with same velocities in the directions shows in figure.
 ABoth the particles will stop momentarily (before striking with ground)at different timesBParticle −1 will rise upto lesser height compared to particle−2CMinimum speed of particle−2 is more than that of particle−1DParticle −1 will strike the ground earlier
ABoth the particles will stop momentarily (before striking with ground)at different timesBParticle −1 will rise upto lesser height compared to particle−2CMinimum speed of particle−2 is more than that of particle−1DParticle −1 will strike the ground earlier
Two particles each of mass m and speed v, travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.
View SolutionTwo particles each of mass m and speed v, travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.
View SolutionPosition vector of centre of two particles of masses m1 and m2 whose position vectors r1 and r2 then rcm?
View SolutionA particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point, its
View SolutionA particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point , its
View Solution
