In the figure d shown a hole of radius 2 cm is made in a semicircular disc of radius 6π cm at a distance of 8 cm from its centre . The distance of centre of mass of this system from centre C is : -

A
4 cm
B
8 cm
C
6 cm
D
12 cm
Text Solution
The correct Answer is:B
Xshift=r2dR2−r2,d=R−2rπ
|
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - III
43 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
Knowledge Check
In the figure shown a hole of radius 2 cm is made in a semicircular disc of radius 6π at a distance 8 cm from the centre C of the disc. The distance of the centre of mass of this system from point C is :
 A4 cmB8cmC6 cmD12 cm
A4 cmB8cmC6 cmD12 cmFind distance of centre of mass of solid hemisphere of radius 8cm from centre
A3 cmB3/8 cmC4 cmD2 cmA circular hole of radius r is made in a disk of radius R and of uniform thickness at a distance a from the centre of the disk. The distance of the new centre of mass from the original centre of mass is
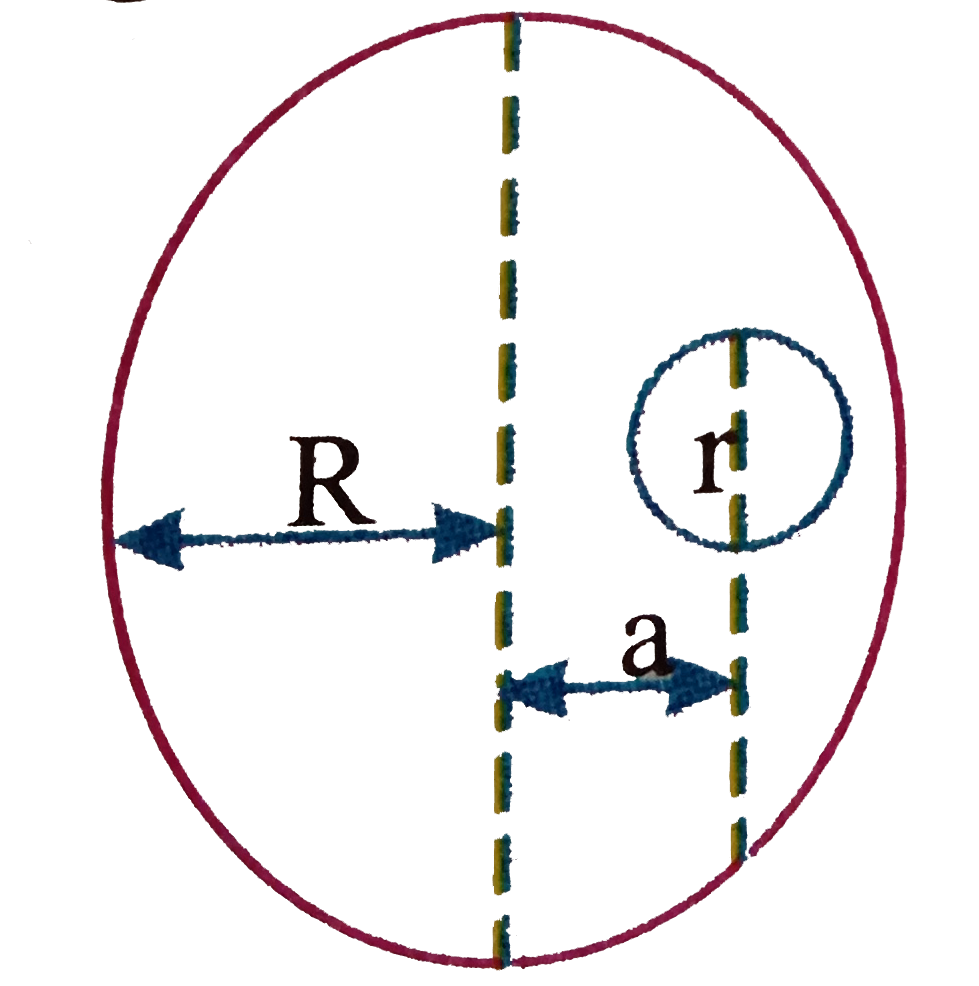 AaR2R2−r2Bar2R2−r2Ca(R2−r2)r2Da(R2−r2)R2
AaR2R2−r2Bar2R2−r2Ca(R2−r2)r2Da(R2−r2)R2
Construct a tangent to a circle of radius 4cm from a point which is at a distance of 6 cm from its centre.
View SolutionFind distance of centre of mass of solid hemisphere of radius 8cm from centre
View SolutionFind distance of centre of mass of solid hemisphere of radius 8cm from centre
View SolutionDraw two tangents to a circle of radius 3.5 cm from a point P at a distance of 6.2 cm from its centre.
View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View Solution
