A ring mass 'm' and radius 'R' has three particles attached to the ring as shown in the figure the cnetre of the ring has a speed V0 . The kinetic nergy of the system in case of no slipping is -

6mV20
12mV20
4mV20
8mV20
The correct Answer is:A
E=22mV20+12m(2V0)2+12m(√2V0)2+122m(√2V0)2
12m(√2V0)2+122m(√2V0)2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - III
43 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
A ring of mass m and radius R has four particles each of mass m attached to the ring as shown in figure. The centre of ring has a speed v0. The kinetic energy of the system is
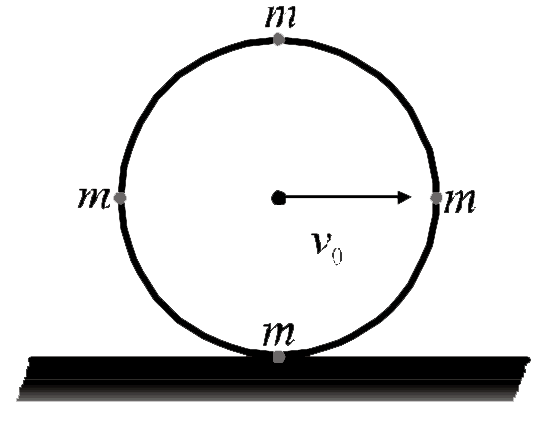
View SolutionA ring mass m and radius R has three particle attached to the ring as shown in the figure. The centre of the centre v0. Find the kinetic energy of the system. (Slipping is absent).
 .
.
View Solution
Knowledge Check
A uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V0. The kinetic energy of the segment ABC is:
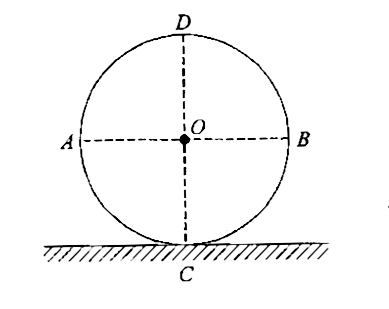 AmV202−mV20πBmv202+mv20πCmv202Dmv20
AmV202−mV20πBmv202+mv20πCmv202Dmv20Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
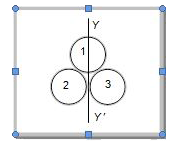 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2Consider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
AGmr2B2Gm√3r2C2Gm3√3r2DGm2r2
A ring mass m and radius R has three particle attached to the ring as shown in the figure. The centre of the centre v0. Find the kinetic energy of the system. (Slipping is absent).
 .
.
View SolutionThree rings each of mass M and radius R are placed in contact with each other as shown . Then MI of the system about YY' axis is

View SolutionFour rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be

View SolutionFour rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be

View SolutionConsider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
View Solution
