The insulated spheres of radii and having charges and respectively are connected to each other. There is
no change in the energy of the system
an increases in the energy of the system
always a decrease in the energy of the system
a decrease in energy of the system unless
The correct Answer is:D
To solve the problem of two insulated spheres with charges Q1 and Q2 connected by a wire, we need to follow these steps:
1. Understand the Setup: We have two insulated spheres, Sphere A with radius R1 and charge Q1, and Sphere B with radius R2 and charge Q2. When connected by a wire, charge will flow between the spheres until they reach the same electric potential.
2. Define Electric Potential: The electric potential V of a charged sphere is given by the formula:
V=kQR
where k is Coulomb's constant, Q is the charge, and R is the radius of the sphere.
3. Set Up the Equation for Equal Potentials: When the spheres are connected, their potentials become equal:
VA=VB
This can be expressed as:
kQ1−qR1=kQ2+qR2
where q is the amount of charge that flows from Sphere A to Sphere B.
4. Eliminate k: Since k is a constant, we can cancel it from both sides:
Q1−qR1=Q2+qR2
5. Cross Multiply: Rearranging gives:
(Q1−q)R2=(Q2+q)R1
6. Distribute and Rearrange: Expanding both sides:
Q1R2−qR2=Q2R1+qR1
Rearranging to isolate q:
Q1R2−Q2R1=q(R1+R2)
7. Solve for q: Thus, we find the charge that has flowed:
q=Q1R2−Q2R1R1+R2
8. Energy Consideration: When the spheres are connected, the energy of the system changes. The energy decreases unless the condition Q1R2=Q2R1 holds true. This condition means that there is no net charge flow, and thus no change in energy.
9. Conclusion: Therefore, the correct statement regarding the energy of the system is that there is a decrease in energy unless Q1R2=Q2R1.
Final Answer
The correct option is:
A decrease in energy of the system unless Q1R2=Q2R1.
V=kQR
where k is Coulomb's constant, Q is the charge, and R is the radius of the sphere.
VA=VB
This can be expressed as:
kQ1−qR1=kQ2+qR2
where q is the amount of charge that flows from Sphere A to Sphere B.
Q1−qR1=Q2+qR2
(Q1−q)R2=(Q2+q)R1
Q1R2−qR2=Q2R1+qR1
Rearranging to isolate q:
Q1R2−Q2R1=q(R1+R2)
q=Q1R2−Q2R1R1+R2
The correct option is:
A decrease in energy of the system unless Q1R2=Q2R1.
Similar Questions
Two non-conduction hollow uniformly charged spheres of radil R1 and R2 with charge Q1 and Q2 respectively are places at a distance r. Find out total energy of the system.

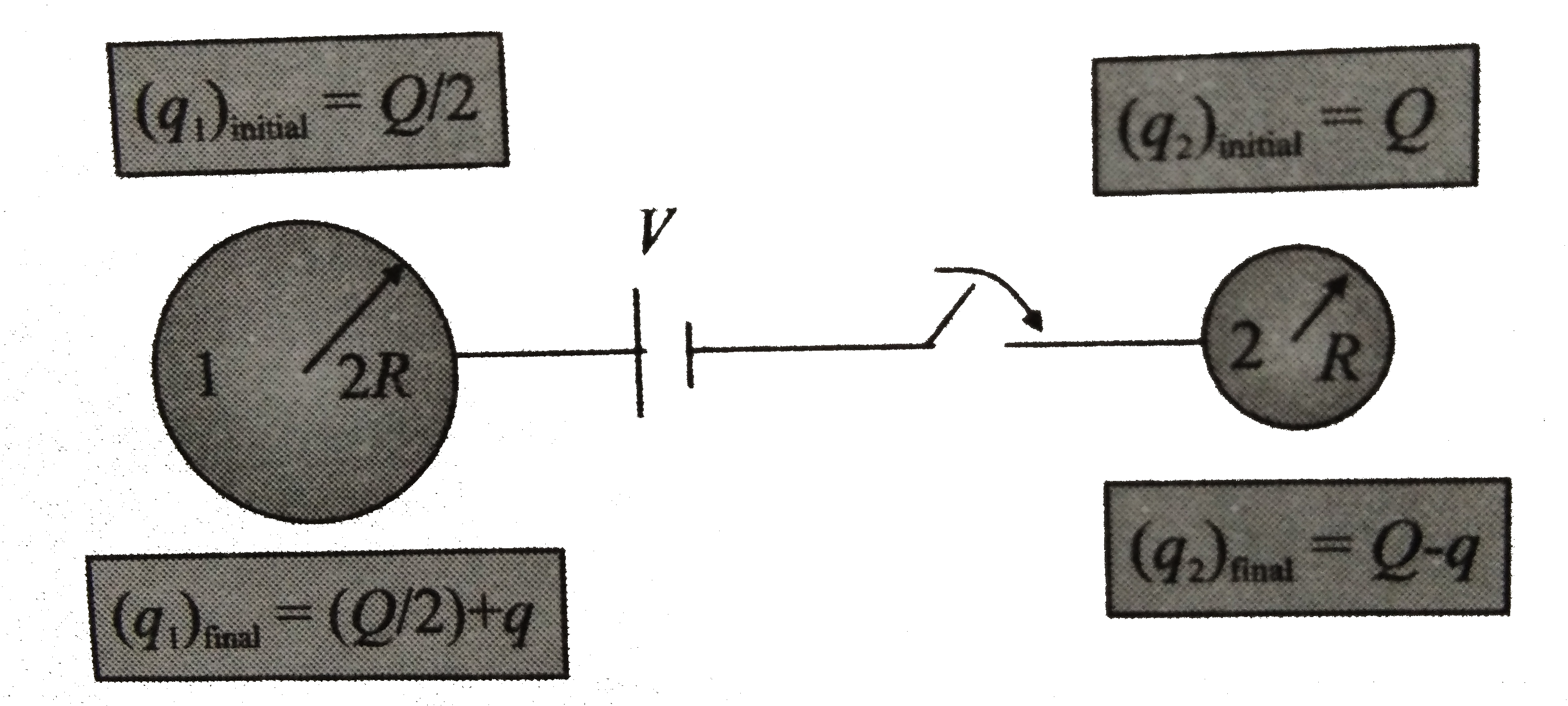
View SolutionThere are two spheres of radii R and 2R having charges Q and Q/2, respectively. These two spheres are connected with a cell of emf V volts as show in. When the switch is closed, find the final charge on each sphere.
View SolutionTwo concentric, thin metallic spheres of radii R1andR2(R1>R2) charges Q1andQ2 respectively Then the potential at radius r between R1andR2 will be (k=1/4π∈)
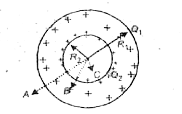
View SolutionYou are given two concentric charged conducting spheres of radii R1andR2 such that R1>R2, having charges Q1andQ2 respectively and uniformly distributed over its surface. Calculate E and V at three points A, B , C whose distances from the centre are rA,rBandrc respectively as shown in figure.
View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionFind force acting between two shells of radius R1 and R2 which have uniformly distributed charges Q1 and Q2 respectively and distance between their centres is r.

View SolutionTwo concentric uniformly charge spherical shells of radius R1 and R2(R2>R1) have total charges Q1 and Q2 respectively. Derive an expression of electric field as a function of r for following positions.
(i) r<R1 (ii) R1≤r<R2
(iii) r≥R2

View SolutionConcentric metallic hollow spheres of radii R and 4R hold charges Q1andQ2 respectively. Given that surface charge densities of the concentric spheres are equal, the potential difference V(R)−V(4R) is :
View SolutionTwo concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
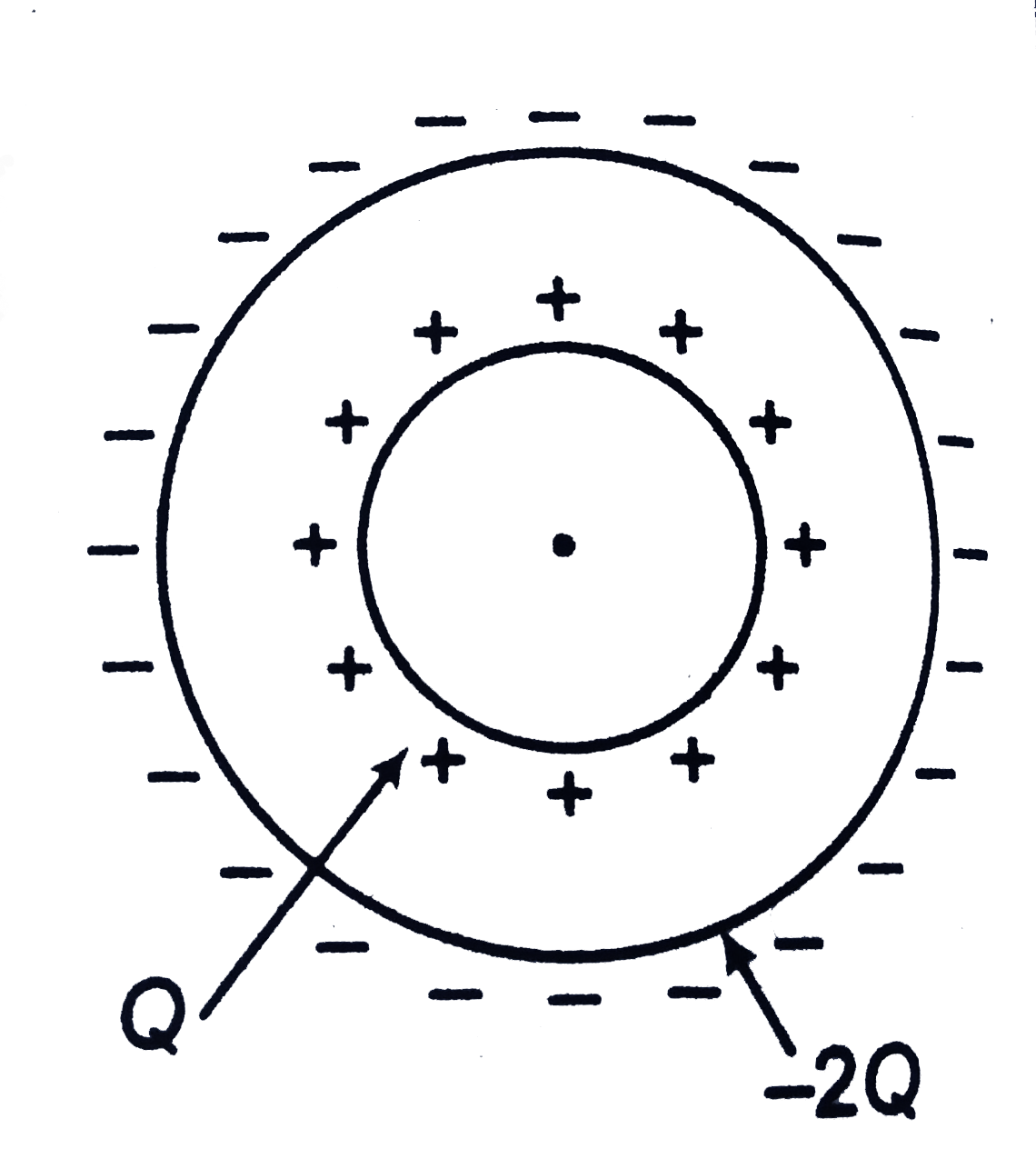
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
View Solution
